Exercises and Discussion Questions
These answers to exercises and discussion questions provide insight into applying the concepts in the text to the scenarios provided.
1.1 A large school district plans to survey parents to measure their opinions on various issues. The survey will be done as follows. A random sample of 20 elementary schools, 10 middle schools and 5 high schools will be drawn. Within selected schools, classes will be randomly drawn: 5 rooms per elementary school, 10 homerooms per middle school and 20 homerooms per high school. A self-administered questionnaire and envelope will be placed in the “home communication” folder of each student in selected classes. Parents will be asked to complete the questionnaire, seal it in the envelope, and send it back to school with their child. Is this an EPSEM sampling procedure? What is the probability of any given student being selected?
For any given student, the probability of being selected is: a) the probability that their school is selected, multiplied by b) the probability that their classroom/homeroom is selected if their school is selected, multiplied by c) the probability that the student is selected if their room is selected.
For any given elementary school student – in the jth room of the kth school – the probability of selection is:
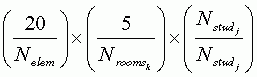
Where Nelem is the number of elementary schools in the school district, Nroomsk is the number of classrooms in the kth school (the student’s school), and Nstudj is the number of students in the jth room of that school (the student’s classroom). There are 20 chances any given elementary school will be chosen, 5 chances that any given classroom will be chosen within a selected school, and if a given classroom is selected, all students in that room will be selected. The last term simplifies to 1; if the student’s room is selected, the student’s chance of selection within the room is 1 (or 100%). Overall, the probability can be reduced to:
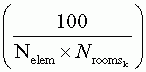
For any given middle school student, the probability of selection is:
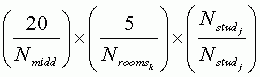
Which reduces to:
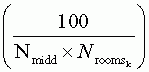
And for any given high school student, the probability of selection is:
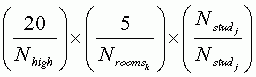
Which reduces to:
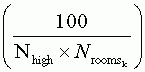
This is not likely to be an EPSEM sample. Within elementary schools, students do not have equal probabilities of selection unless every elementary school has the same number of classrooms (i.e., ![]() is constant across schools); otherwise, students at schools with more classrooms have a lower chance of selection. The same applies within middle schools and high schools. Then, even if all schools within each category have the same number of rooms, students will not have equal probabilities of selection across categories unless the denominators of the reduced expressions are equal; that is, unless the number of schools times the number of rooms per school – i.e., the total number of rooms – is the same for all three categories (elementary, middle, and high).
is constant across schools); otherwise, students at schools with more classrooms have a lower chance of selection. The same applies within middle schools and high schools. Then, even if all schools within each category have the same number of rooms, students will not have equal probabilities of selection across categories unless the denominators of the reduced expressions are equal; that is, unless the number of schools times the number of rooms per school – i.e., the total number of rooms – is the same for all three categories (elementary, middle, and high).
1.2 A university wants to learn about the problems its freshmen experience in making the transition to college, so it can design and prioritize programs to keep these students in school. The university plans to gather this information from freshmen who sign up for interviews in exchange for extra credit in an Introduction to Psychology class. How do you evaluate this sample in terms of potential coverage bias, selection bias, and non-response bias? Overall, is this sample acceptable for the research purpose? Would the university do better if it sent a request to freshmen’s e-mail addresses asking them to participate in the research, and collected the information online?
In evaluating this sample for possible coverage bias, the key question is: who takes Introduction to Psychology (or more specifically, who takes this class as a freshman, assuming that only freshman will be eligible for the research)? Is it required for all students at this school? Is it required for social science majors, but not engineers? Even if it is required for engineers, do they take it during their freshman year, or do they postpone it while they focus on math and science requirements, while social science majors take the course as freshmen? It is easy to imagine this class having disproportionate coverage across majors, and perhaps missing some majors entirely. Within majors, are the students who take this class different from those who don’t? For example, if engineers are underrepresented, are the engineers who take this class similar to those who don’t, so we can adjust for the underrepresentation by simply weighting the data (we discuss weighting in Chapter 7), or do differences exist between the engineers who take this class as freshman and those who don’t?
Regarding possible selection bias, this will be a “volunteer sample.” The key question is whether the students who participate in this type of interview for extra credit are different from those who don’t. Do virtually all students who take this course participate in research for extra credit? Do students sign up for projects based on their interest in the listed topic, or do they simply take whatever project fits their schedule?
Regarding non-response bias, there should be very little non-response; virtually every student who volunteers to participate in exchange for extra credit is likely to complete the interview. This is a case where a high response rate tells us very little about the quality of the sample, because the participants are volunteers.
Overall, we can see reasons why this sample may be biased, with the extent of potential bias depending on the answers to the questions we raised. We will have less concern if Intro Psychology is required of all freshmen, virtually everyone in the class participates in extra credit projects, and students choose projects based on convenience rather than interest – more concern if the course is taken mostly by psychology majors and students volunteer for projects based on interest in the topic. Either way, we will only be able to judge the potential for sample bias. We won’t know the extent of actual bias of bias (if any) unless we gather data from this sample and compare it with a random sample of freshman.
This brings us to the question of whether the sample is acceptable for the research purpose. The answer depends on two things: a) the general extent to which the sample has potential bias, as discussed above, and b) the extent to which the possible sources of bias are problematic given the specific purpose(s) of the research.
Here, the university wants to learn about the problems its freshmen experience in making the transition to college, so it can design and prioritize programs to keep these students in school. To the extent the focus is simply on identifying possible transition problems, we might feel that almost any sample that contains a wide swath of freshmen is acceptable, because a broad sample of students will allow a broad set of problems to surface. If Introduction to Psychology draws freshmen from all over campus, and participation in the research is not based on specific interest in the topic, then interviews with Intro Psych students may be an inexpensive way to identify possible problems and begin to learn what kinds of students have what kinds of problems. On the other hand, if the focus of the research is on quantifying how many students have various problems, so as to prioritize the problems, then we might be more concerned about the extent to which various types of students are not just present in the sample, but are proportionately represented.
Similarly, to the extent the research is focused on social variables such as being away from home and friends, almost any sample of freshmen may be acceptable (at least if it covers a mix of housing arrangements such as dormitory versus fraternity or sorority), because these issues are likely to be common across groups of students. To the extent the research is focused on academic variables such as difficulties in doing college-level math or keeping up with reading assignments, the mix of majors may be more important.
Would the university do better if it sent a request to freshmen’s e-mail addresses asking them to participate in the research, and collected the information online? The answer is maybe. Assuming that all freshmen provide or are assigned an e-mail address, the e-mail addresses would provide complete coverage of the population, hence no coverage bias. If a request to participate is sent to all of those e-mail addresses, or a random sample of addresses, there should be no selection bias. However, non-response might be a major problem. Students might not check their e-mail during the survey period, might delete the request without opening it, might click through and decide the survey does not apply to them, or might start the survey and break off if they get tired of it. The result might be a sample that is more engaged in campus life (and has fewer transition problems) or a sample that is particularly interested in the topic (and has more transition problems). Judgments about the extent and nature of potential sample bias will depend on the response rate and the extent to which non-response takes the form of not clicking through to the questionnaire as opposed to clicking through and abandoning. As with a sample of volunteers from Intro Psych, we will only be able to judge the potential for sample bias, not the extent of actual bias.
Ultimately, the choice of a sampling procedure in this example will depend on factors such as population coverage in the Introduction to Psychology class, expected response rate from an e-mail sample, length of the questionnaire (which may affect the e-mail response rate), and perhaps most important, the specific objectives of the research. You also may see additional issues that we have not raised. As this example illustrates, sampling decisions are often based on practical considerations, not just fine points of technique, and imperfect samples may be deemed usable for the purposes at hand. See Chapter 9 for further discussion of “how good must the sample be.”
