Exercises and Discussion Questions
4.1 A hospital administrator is planning a patient satisfaction survey. She wants to know the proportion of patients, among a population of approximately 5,000 treated at the hospital during the past three months, who say they were "completely satisfied" with various aspects of the hospital's performance. She wants to be 95% confident that her estimates fall within ±.04 (±4%) of the population figure for each measure. How big a sample does she need? If she wanted a confidence interval of ±1% (instead of 4%) for the same estimates, how big a sample would she need?
We use Equation 4.3 to solve for n. That equation is:
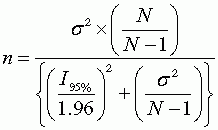
Substituting {π * (1 – π)} for σ2, setting π equal to .5 because this yields the most conservative result, and setting the desired confidence interval to ±.04, we get:
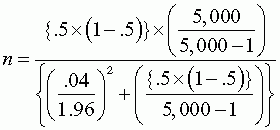
Setting the confidence interval to ±.01, we get:
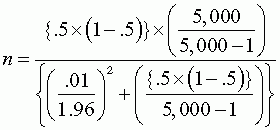
4.2 Given the information in Section 4.4.1, what would be the value of research if the manager never changed her mind, and had the same 65% hit rate with or without information? What if the research improved the hit rate to 85%? What if the potential gain from each decision was $10,000 and the potential loss was $10,000?
If the manager never changed her mind, and had the same 65% hit rate with or without information, then the value of research would be zero. Without research, being right 65 times in 100 decisions makes the firm $65,000,000, while being wrong 35 times loses $35,000,000, for a net profit of $30,000,000. If the manager has the same 65% hit rate with research, the profit will remain at $30,000,000 and there will be no gain. The difference between the firm's profits with and without research is $30,000,000 – $30,000,000 = $0. This illustrates that information only pays off when decision-makers change their minds.
If research improves the hit rate to 85%, the net profit will go to $85,000,000 – $15,000,000 = $70,000,000. The difference between the firm's profits with and without research will be $70,000,000 – $30,000,000 = $40,000,000, or $400,000 per decision. This illustrates that the value of information depends on the extent to which it improves decisions.
If research improves the hit rate to 75% as in the example, but the potential gain from each decision is $10,000 and the potential loss is $10,000, then the value of information changes as follows. Without research, being right 65 times in 100 decisions makes the firm $650,000, while being wrong 35 times loses $350,000, for a net profit of $300,000. With market research, and a 75% rate of correct decisions, the net profit is $750,000 – $250,000 = $500,000. The difference between the firm's profits with and without research is $200,000, or $2,000 per decision. This illustrates that the value of information depends on the gains or losses at stake.
4.3 A college instructor is planning a class project that involves a telephone survey. The instructor has 40 students in the class, and wants each student to do a reasonable number of interviews for the project within a two-week period. What would be a reasonable number of interviews for each student to do? What is the resulting sample size?
There is no set answer to this question; it all depends on what the instructor considers reasonable, which in turn may depend on the quality of the list and/or rareness of the population (hence how many calls it takes to find an eligible respondent), and the availability and cooperativeness of the population (hence how many eligible respondents it takes to produce an interview). Just as an example, if the students can complete 10 interviews each on average, the sample size will be 400 (40 students times 10 interviews per student). If the students can complete 5 interviews each on average, the sample size will be 200. This illustrates sample sizes based on resource limitations.
