Exercises and Discussion Questions
5.1 Refer to Tables 5.1 and 5.2. In Table 5.2, the first two columns show sample allocations based on proportional allocation and σh for payroll, and the resulting sampling variances for payroll and number of employees. How would these numbers change if the number of hospitals with less than 50 beds, shown in Table 5.1, was 2,614 instead of 1,614?
If the number of hospitals with less than 50 beds, shown in Table 5.1, was 2,614 instead of 1,614, the first two columns in Table 5.2 would change as follows:
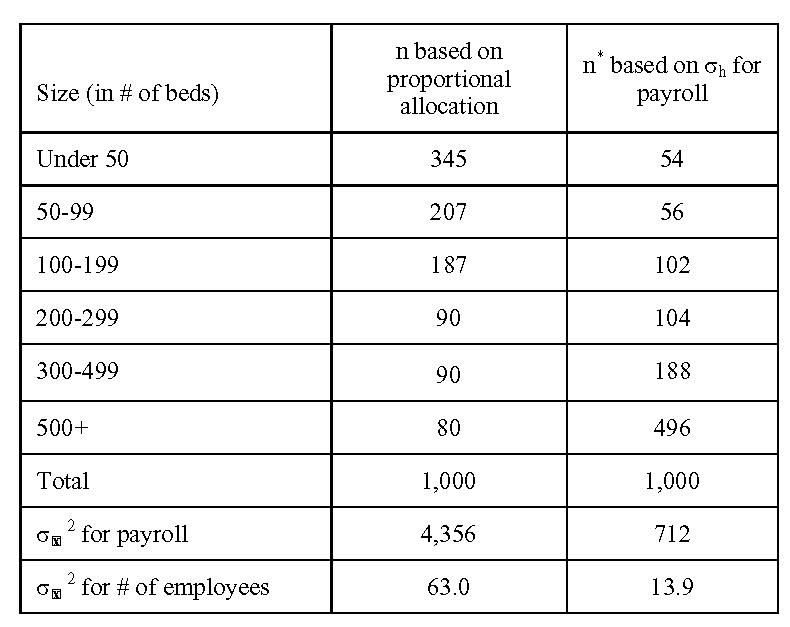
Compared with Table 5.2, relatively more sample is allocated to hospitals with less than 50 beds, because they now account for a larger proportion of the population.
Following Equation 5.1, the sampling variances for payroll and number of employees are calculated as:
![]()
Don’t forget to use the finite population correction in calculating the ![]() terms. It will make a difference, especially for hospitals with 500+ beds, because our disproportionate sample allocation for that stratum (n*) represents more than 80% of the stratum population.
terms. It will make a difference, especially for hospitals with 500+ beds, because our disproportionate sample allocation for that stratum (n*) represents more than 80% of the stratum population.
If you get numbers that are close to these, but a little different, the difference is probably just from rounding effects.
5.2 Following the example given in Section 5.1.3, assume that some Hispanics in a region live in areas that are 100% Hispanic, while others live in areas that are only 2% Hispanic. Assume that the cost of each interview is $25 and that screening households to determine if they are Hispanic costs $10 per screen. What should be the sampling rate in areas where Hispanics are rare compared with the areas that are entirely Hispanic?
Given these numbers, the total cost per completed case is $35 in the areas that are 100% Hispanic, since each $10 screening call will lead to a $25 interview, and $525 in the areas that are only 2% Hispanic, since there will be 50 screening calls at $10 per case for each completed interview. Since Ö($35/$525) is .258, the sampling rate in those areas where Hispanics are rare should be 26% (or roughly one-fourth) of that in the areas that are entirely Hispanic.
