Calculating weighted means to combine effect sizes from different studies (for Intermezzo 3)

Calculating a mean value from a set of values is easy. We add up the set of numbers and then divide by n, the number of values. This is written as a formula:

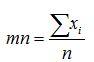
where mn is just shorthand for ‘mean’ and x_i indicates each individual value.

A more general version of this formula allows us to give more weight to some values than others, instead of treating each value equally. We suppose that for each value, x_i, we also have weight, w_i, which is larger the more weight we wish that value to have in the mean. Then the formula becomes this:

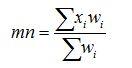
where w_i indicates the weight of each value.

It does not take too much work to notice that, if all the weights are equal to 1, then this formula becomes the same as the one above it. Firstly, multiplying anything by 1 doesn’t change it, so x_iw_i is the same as just x_i when w_i is equal to 1; and because the sum of a set of weights where each weight is equal to 1, equals n.

When we use this approach to combine effect sizes from different studies, we will want to give a weight to each study that reflects its quality. While the simplest way to imagine weighting is to imagine it with regards to sample size, where a larger sample reflects more “weight” for a particular study, weighting is better done by taking uncertainty into consideration instead. Typically, this involves weighting the effect size from each study by the inverse of the uncertainty associated with that study. The inverse of a value is one divided by that value:

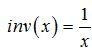
As a simple example, the inverse of 4 would be 1 divided by 4 (or 0.25). As we know from previous chapters, the standard error is a good measure of the uncertainty in the study, so we weight each study by the inverse of its standard error. So, the overall effect size is then given by this formula:

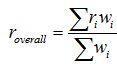
where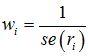 

An example

Let’s imagine that we have three studies. Their effect sizes and standard errors are listed in the Table below. To find ‘r overall’ which is our combined effect size, we need the sum of each effect size multiplied by its “weight” (as per the top line of the formula), divided by the sum of the “weight” values.

Taking all these values and looking at the formula, we now have a value for the top row, and a value for the bottom row. We have found that Σ r_iw_i is equal to 17.15, and that Σ w_i is equal to 53.08. When we divide 17.15 by 53.08, the result – our weighted effect size – is 0.32. We can compare that to the normal mean of the three effect sizes, which is 0.27; quite a difference.