Answers for Data Skill Challenges for every chapter in the book can be found to check your performance and widen your understanding.

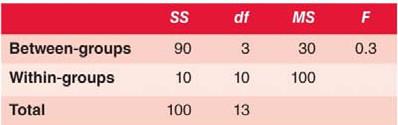
1)      F_crit(3, 10) = +3.71

F(3, 10) = 0.3, p >.05

Figure 10.1

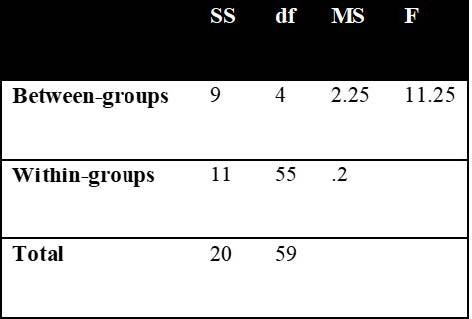
2)      F_crit(4, 55) = +2.56

F(4, 55) = 11.25, p < .05

Figure 10.2

3)      Figure 10.3

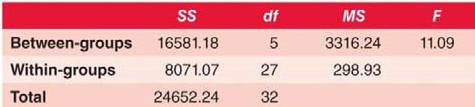
RQ: Do any of the website designs produce different viewing times from the other website designs?

H₀: μ₁ = μ₂ = μ₃ = μ₄ = μ₅ = μ₆

H₁: At least two means differ

α = .05

F_crit(5, 27) = +2.57 (Excel) or F_crit(5, 27) = +2.76 (by hand)

F(5, 27) = 11.09, p <.05

η² = 0.67

Conclusion: Reject the null and accept the alternative. The ratio is statistically significant. At least two website designs have different means. Website design accounts for 67% of the total variance in viewing times. In post-hoc analyses, three homogeneous subgroups were identified. The first subgroup, containing Designs B, E and H, resulted in longer viewing times than the second subgroup, containing Designs B, C, E and F, which resulted in longer viewing times than the third subgroup, containing Designs C, F and G.

4)      Figure 10.4

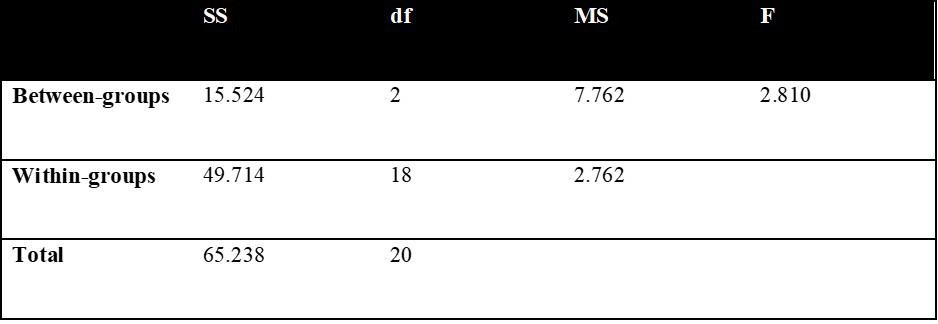
RQ: Do customers tip differently depending on the time of day?

H₀: μ₁ = μ₂ = μ₃

H₁: At least two means differ

α = .05

F_crit(2, 18) = +3.55

F(2, 18) = 2.81, p > .05

Conclusion: Retain the null. The ratio is not statistically significant. There is not sufficient evidence to conclude that customers tip differently based on time of day.