Chapter 2: Mathematical Foundations
2.8 Problems and Exercises
1. For the types of relations listed in Problem 3 in Chapter 1, are the ties implied by these relations directed or undirected?
b. Financial transactions among banks
c. Preschool children’s stated play preferences
d. College student attendance at university functions
e. Who one trusts in an organization
f. Advice-seeking among scientific research team members
g. Who one talks to about important matters
h. Money lending in a rural Indian community
i. Conflict among ethnic groups in South Sudan
j. Enjoys working with in small project teams
k. Would want to work on future projects with others in a high tech firm
l. Sexual relationships among IV drug users
m. Lab proximity of scientists in a research institute
n. Observed interactions at a company picnic
o. County commissioners and their votes on policy issues
2. Re-express the simple graph below as an adjacency matrix.
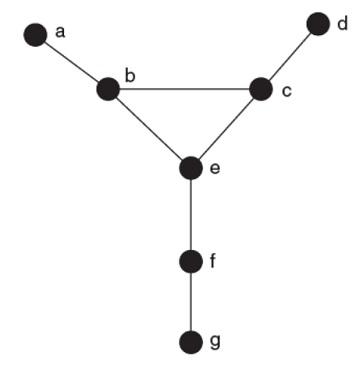
Graph as adjacency matrix

3. Re-express the graph in problem 2 as a geodesic distance matrix. What do those distances mean?
The distance on the shortest path from i to j.
Geodesic distance matrix

4. For the graph in Problem 2 above, provide examples of each of the following:
5. Re-express the directed valued graph below as a valued proximity matrix.
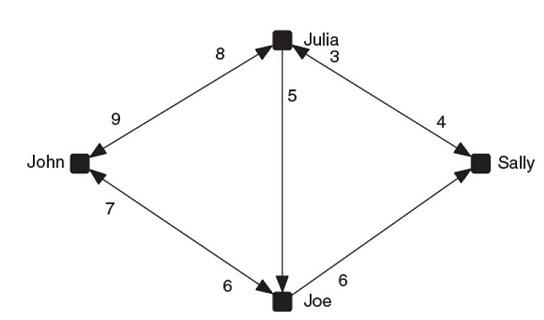
Valued proximity matrix

6. For the bank wiring room games graph in Figure 2.2a, if the edge between nodes W7 and W5 were removed, how many components would the graph now have? If we were to calculate geodesic distances for the new graph, what would be the distance between W9 and W3? Explain.
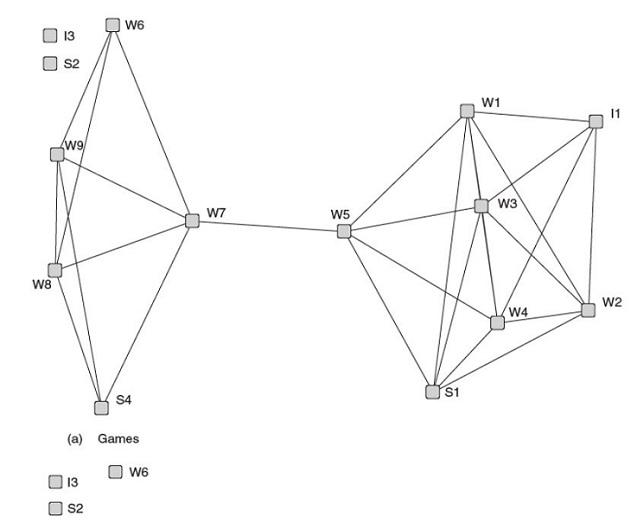
Answer: Once the edge between W7 and W5 is removed there are now 4 components, two larger components and two isolates.
Answer part 2: The distance between W7 and W5 once the edge is removed is undefined or infinite (i.e., there is no path by which W7 can reach W5 and vice versa)
7. For each of the network examples in Chapter 1, Problem 3, are the associated matrices one-mode or two-mode?
b. Financial transactions among banks
c. Preschool children’s stated play preferences
d. College student attendance at university functions
e. Who one trusts in an organization
f. Advice-seeking among scientific research team members
g. Who one talks to about important matters
h. Money lending in a rural Indian community
i. Conflict among ethnic groups in South Sudan
j. Enjoys working with in small project teams
k. Would want to work on future projects with others in a high tech firm
l. Sexual relationships among IV drug users
m. Lab proximity of scientists in a research institute
n. Observed interactions at a company picnic
o. County commissioners and their votes on policy issues
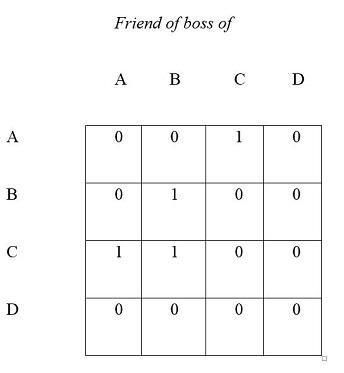
8. Given a friendship relation and ‘is the boss of’ relation, use matrix multiplication to hand-calculate the “is friends with the boss of” relation.
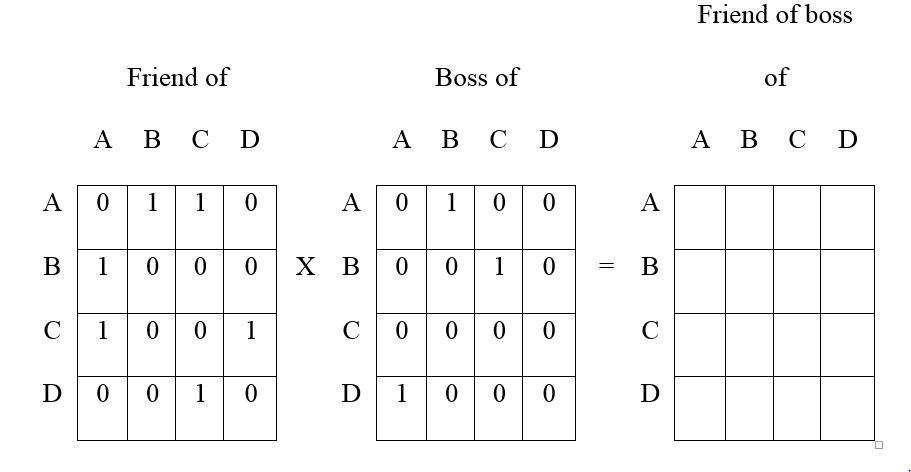
Recall that if cell (A,C) has a value greater than zero in the ‘is friends w/ the boss of’ matrix, it means that A is friends with C’s boss. From a power perspective, how would you view the row sums of the ‘Friend of boss of’ matrix?
A high row sum means that the row person is friends with lots of people’s bosses. They are in a position to shape the bosses’ perceptions of their subordinates positively or negatively. Either way, the persons with larger row sums have potential influence. The subordinates would do well to recognize this source of influence on their bosses.