Student Resources
Chapter 4 – Mathematical language, reasoning and proof
Consider the following statements and click to reveal the answer.
1. (a) Prove that the sum of the interior angles of a quadrilateral is always equal to 360°. (You may assume the sum of the angles of a triangle.)
(b) Suggest an approach to this in which children use inductive thinking.
Answer:
(a) A quadrilateral can always be divided into two triangles, e.g.:
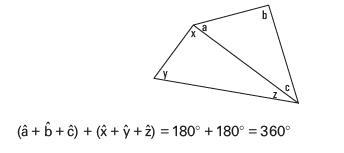
But, the four angles of the quadrilateral are also the sum of these six angles.
(b) Children could either draw several quadrilaterals, measure the angles and find the sum, or, tear off the corners and show they fit together to make one rotation.
2. Prove that (a) the product of two even numbers is even, and (b) the product of two odd numbers is odd.
Answer:
(a)Our two even numbers can be written, 2a and 2b, where a and b are integers. Multiplying gives:
2a × 2b = 2(2ab)
2ab is the product of three integers and must also be an integer (an assumption). Hence 2(2ab), the product of two even numbers, must be even.
(b) Writing our odd numbers as 2a + 1 and 2b + 1 and multiplying gives:
(2a+1)(2b+1) = 4ab + 2b + 2a + 1
The final unit makes it impossible to divide this expression by 2, so it is not even. Therefore, the product of two odd numbers is odd..
3. Prove that the product of three consecutive numbers is even.
Answer:
Three consecutive numbers must contain at least one even number of the form 2a, where a is an integer. The product of 2a and any other two integers gives a number divisible by 2, hence the product is always even.
4. Prove by exhaustion that there are only six ways of listing the letters a, b and c.
Answer:
Undertaken systematically, the possibilities are:
abc bac cab
acb bca cba
5. Find counter-examples to refute these assertions:
(a) Multiplying makes a number larger.
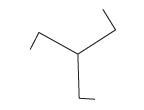
(b) If a shape has rotational symmetry, it also has reflective symmetry.
(c) If a and b are both
Answer:
(a) 0.1 × 60 = 6 or 12 10 5×= would do.
(b) This shape or variations on it would refute
(c) 8 and 6 are both factors of 24, but 8 is not a factor of 6 and 6 is not a factor of 8.
6. Prove that for any chord, AB, angles â and bˆ are equal. List any assumptions you make.
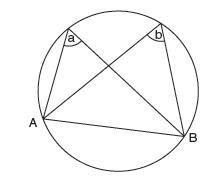
Answer:
Assuming the truth of the theorem that the angle subtended at the centre is twice that at the circumference, we can argue:

7. List three standard methods of proof that could be used in primary schools.
Answer:
Three standard methods of proof that could be used in primary schools are:
deductive proof;
disproof by counter-example;
proof by exhaustion.
8. What are the three ways in which we can represent mathematical ideas?
Answer:
The three ways in which we can represent mathematical ideas are:
- language describing using words, phrases and sentences;
- through the use of pictures/objects including number lines and mathematical apparatus;
- using specialist symbols.
9. What do the following abbreviations mean?
(a) OE
(b) ME
Answer:
The following abbreviations mean:
(a) OE Ordinary English;
(b) ME Mathematical English.
