Chapter 11: Testing for Differences: ANOVA and Factorial Designs
Short answer questions.
1. From the model approach we have used, what are the components of an individual score in a 2X2 factorial design? Assume both factors are between-subject in nature.
Main Points:
- Population mean
- True treatment effect of factor 1, if there is an effect.
- True treatment effect of factor 2, if there is an effect.
- True effect of the interaction between factor1 and factor 2, if there is an effect.
- error
2. What is the difference between a main effect and a simple effect? In a factorial design with one between-subject factor and one within-subject factor, how do you test the simple effects for the between-subject factor?
Main Points:
- The Main effect for a factor is based on summing across all levels of the other
- Simple effects for a factor are based on examining separately that factor at each level of the other factor.
- To test the simple effects of the between-subject factor the within-subject and the between subject error terms are combined (both sum-of-squares and degrees-of-freedom).
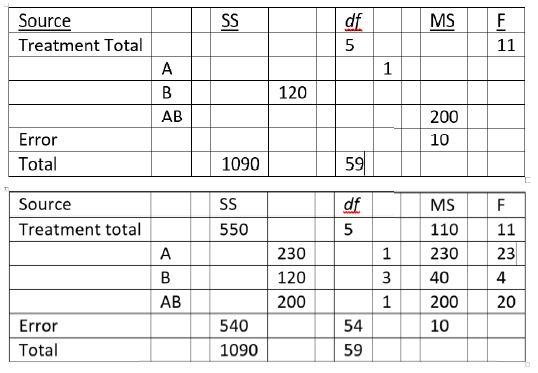
3. Complete the below ANOVA summary table from a factor analysis of a two-way between-subject design.
4. How can a factorial design with one between-subject factor and one within-subject factor be viewed as two one-way ANOVAs? What is the major qualification that must be made?
Main Points:
- The sum-of-squares total is first partitioned into sum-of-squares within-subjects and the sum-of-squares between-subjects.
- Then the ANOVA looks like two one-way ANOVAs with their individual error terms, which have been partitioned.
- The qualification revolves around the interaction treatment term which is now located on the within-subject side of the partition.
5. As more and more of the SStotal are associated with the SSbs, what happens to the statistical power for testing the between-subject and the within-subject effects? Why?
Main Points:
- The sum-of-squares for the treatment terms cannot change.
- As the sum-of-squares between-subjects are increasing it can only mean that there is more and more error on the between-subject side of the partition.
- As error increases on the between-subject side, power must be decreasing.
- The total amount of error is constant.
- As error on the between-subject side of the partition increases, it must be decreasing on the within-subject side.
- Thus, power on the within-subject side will be increasing.
Data questions.
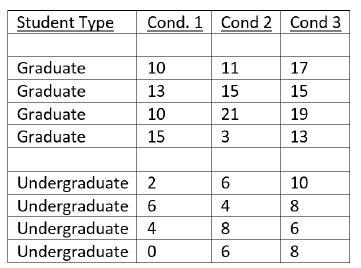
1. A psychologist suspected that sleep prior to a memory test would improve scores for both graduate and undergraduate students, and that within the range examined, the more one sleeps, the more improvement there would be in memory scores. He also thought that in general graduate students would do better than undergraduates on the memory test. To test his hypotheses, he randomly assigned 12 graduate students to 3 conditions: condition 1 (no sleep), condition 2 (4 hours of sleep), and condition 3 (8 hours of sleep) and 12 undergraduates to those same three conditions. Do the below data support his hypothesis? The scores are the number of items correctly recalled. Be sure to include all tests of assumptions (with conclusions), descriptive statistics, appropriate graph, test of null hypotheses, experimental conclusion, as well as the appropriate follow-up (power or effect size) procedures.
Main Points:
Graduate students coded as a 1 and undergraduates coded as a 2.
a. Descriptive statistics.
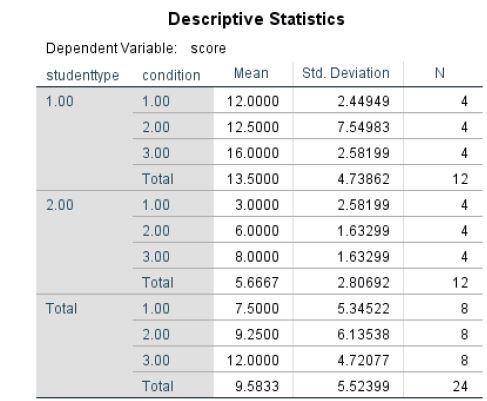
No outliers are found.
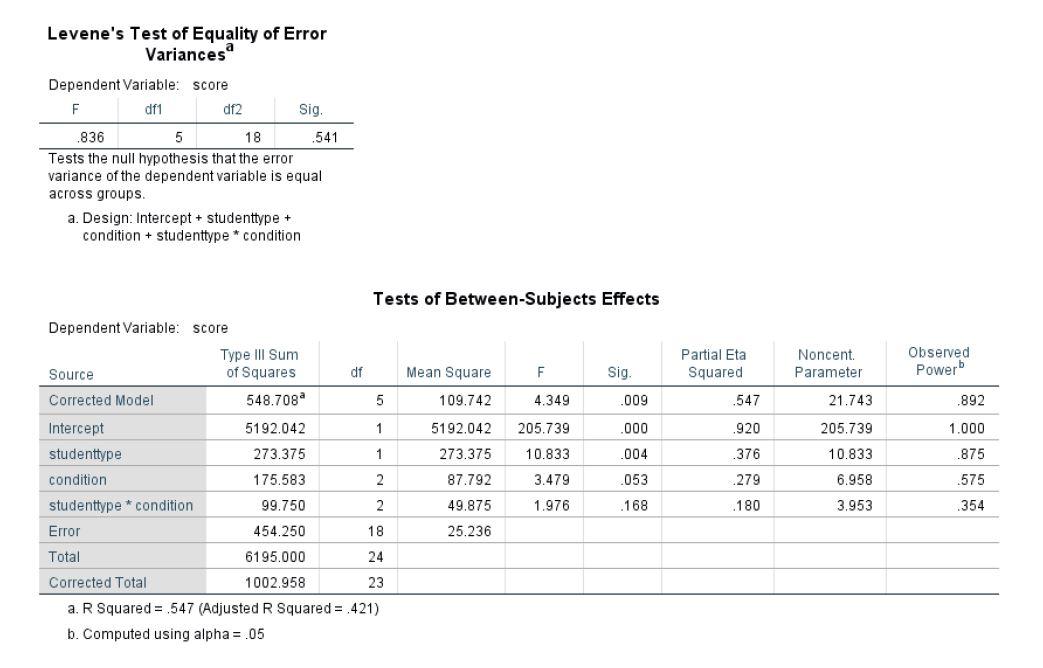
b. Levene’s test of homogeneity of variance.

Could be an issue with homogeneity of variance with p = .041. Might considered alternate form of analysis.
c. Figure.
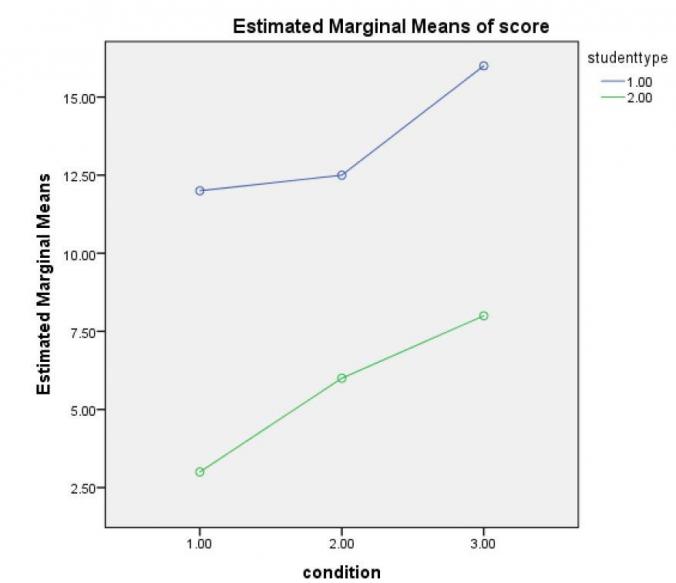
Looks as if the more sleep (condition) the better the memory. Looks as if the graduate students did outperform the undergraduates. There is not much of an indication concerning an interaction.
d. ANOVA output.
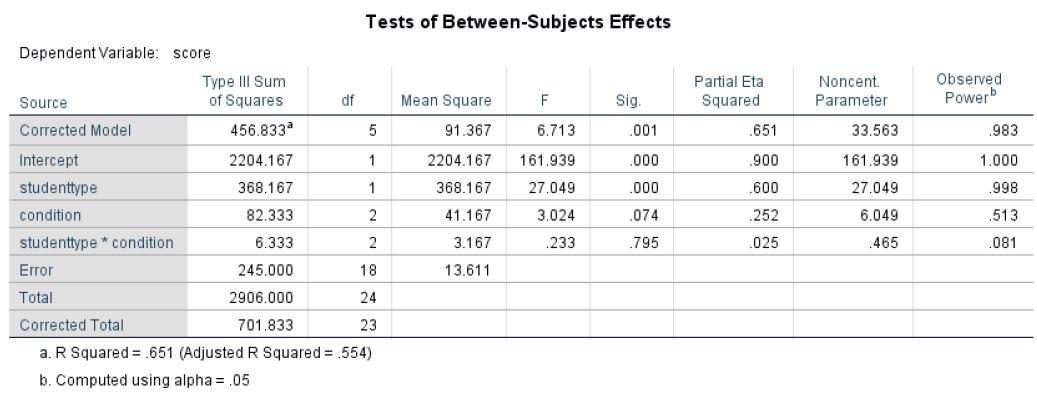
Sleep (condition) was not found to be significant: F= 3.024, MSE = 41.167, p = .074. The observed power for an effect the size observed is .513 (see descriptive statistics for the total panel).
Student type was significant: F= 27.049, MSE = 368.167, p. = 000. The graduate student did outperform the undergraduates. (Partial eta squared = .600, standardized effect size)
The interaction was non-significant: F = .223.
e. The evidence partially supports the researcher’s ideasHowever, there are the issues with power and heterogeneity of variance.
f. Running a Kruskal-Wallis non-parametric results, however, does not change the outcome for the test of the number of hours of sleep (condition).
2. Another psychologist suspected that sleep prior to an abstract reasoning test would improve scores for both graduate and undergraduate students, and that within the range examined, the more one sleeps the more improvement there would be in memory scores. She also thought that in general graduate students would do better than undergraduates on the abstract reasoning test. To test her hypotheses, she tested 4 graduate students in 3 conditions: condition 1 (2 hours sleep), condition 2 (5 hours of sleep), and condition 3 (8 hours of sleep). She also tested 4 undergraduates in those same three conditions. Do the below data support her hypothesis? The scores are the number of items answered correctly. Be sure to include all tests of assumptions (with conclusions), descriptive statistics, appropriate graph, test of null hypotheses, experimental conclusion, as well as the appropriate follow-up (power or effect size) procedures.
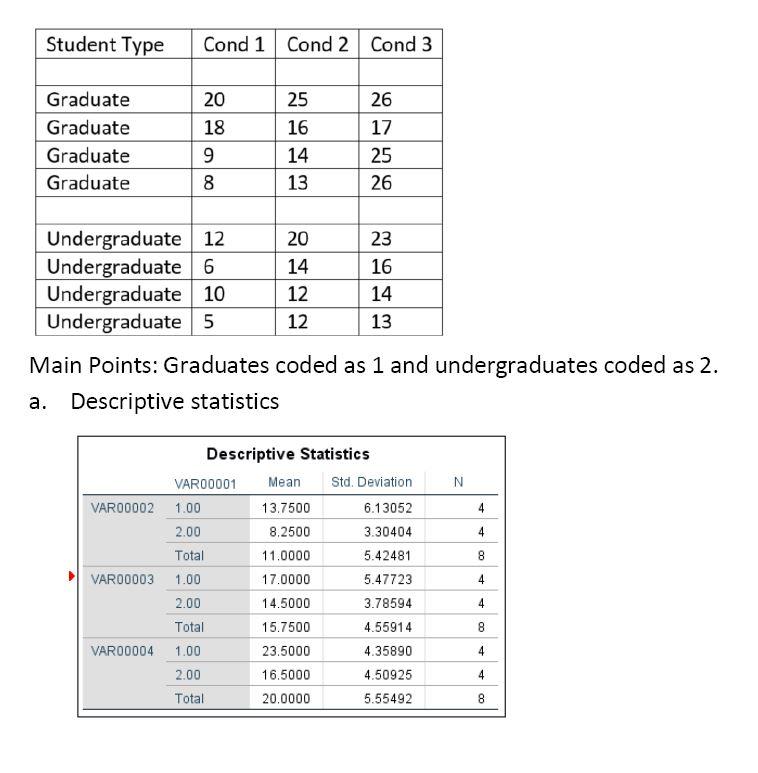
No outliers are found.
b. Figure
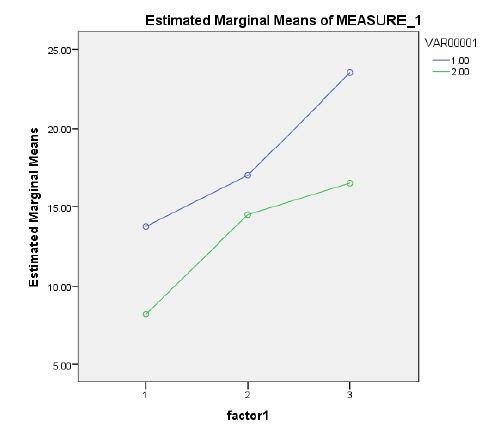
c. Mauchly’s test indicates probably no problem with sphericity (p. = .078).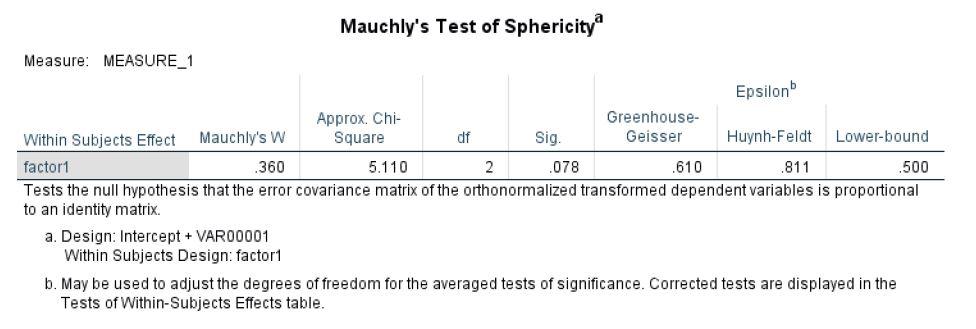
d. Test for within-subject condition (sleep) is significant (p. = .001) (Assuming sphericity).
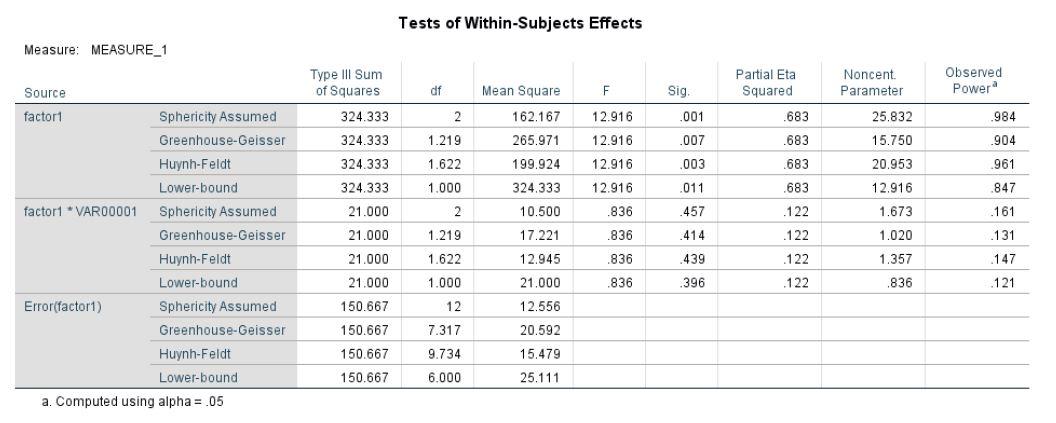
Partial Eta Squared = .683
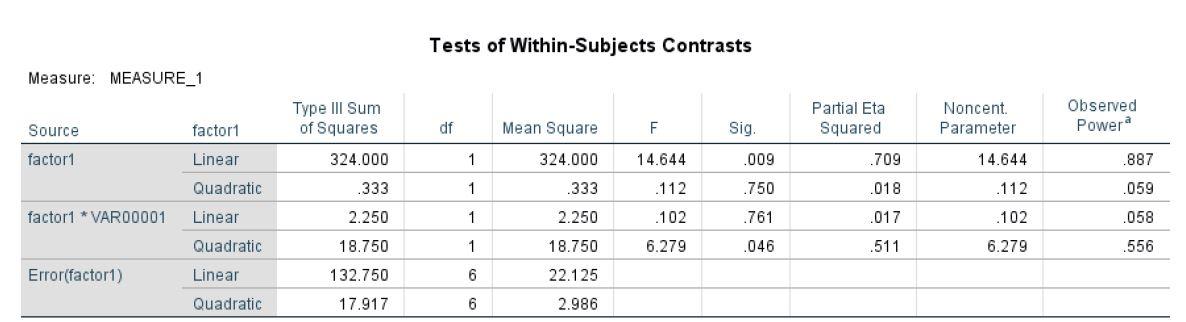
e. The within-subject contrast indicates that score increases linearly as a function of sleep: F = 14.644, p. = .009.
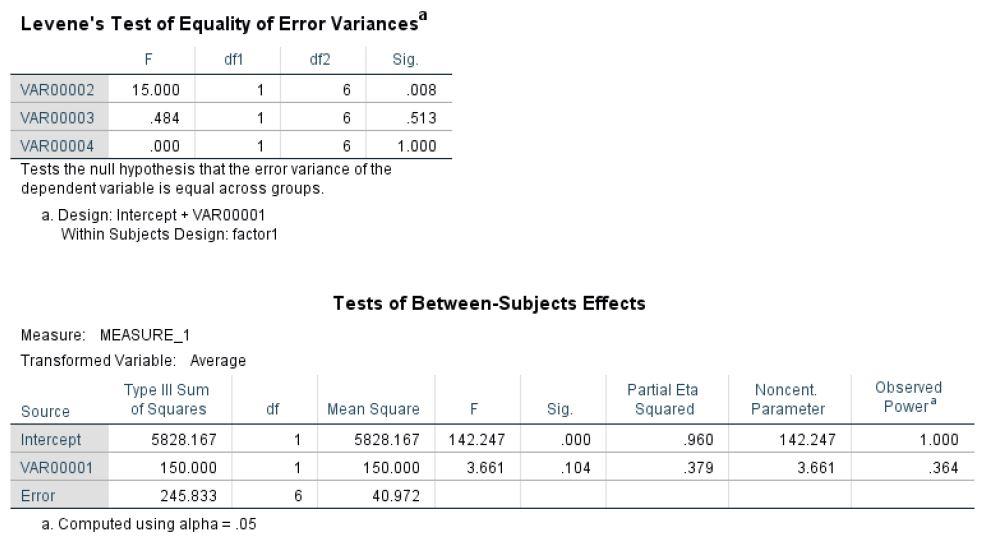
f. Levene’s test indicates a problem with the assumption of homogeneity of variance. The test of the between-subject factor (VAR0001, student type) is non-significant : F= 3.661, MSE = 150.00, p. = .104). The observed power is weak (.364), however.
g. Again, because of the problem of heterogeneity of variance, you may consider switching the analysis to non-parametric. The results, however, will not change.
h. The results partially support the researcher’s hypotheses.
3. An error has been made regarding the design of the experiment in the above question concerning abstract reasoning. The design was not one between-subject variable (graduate versus undergraduate students) and one within-subject variable (hours of sleep). Both variables were between-subject in nature. There were 12 graduate students and 12 undergraduate students. Rerun the complete analysis. What differences are there? Why?
Main Points:
a. Descriptive statistics do not change. It is still the same data.
b. Levene’s test changes to being non-significant. (No longer is the total error partitioned into between-subjects and within-subjects. Student type remained significant. Condition and the interaction terms remained non-significant. The condition term almost reached significance with its increase in power.