11.1 MS_error and MS_treatment are the same in that they both estimate the true population variance if the null hypothesis is true. Both MS_error and MS_treatment are unbiased estimators of the true population variance. If the null hypothesis is false, MS_error remains an unbiased estimator of the true population variance. Any treatment effect does not affect the within-condition variances. However, when the null hypothesis is false, MS_treatment will contain at least one more constituent of constituent or ‘source’ of variance and will no longer be an unbiased estimate of the true population variance. If there is no confounding variable, the source of this additional constituent of variance is attributed to the independent variable.

11.2 The MS_error for a one-way independent-samples ANOVA is the average within-condition variance. Because all of the condition variances in Figure 11.3 are 1.0, the MS_error for the ANOVA will be 1.0.

11.3 The MS_error was already completed by you in the previous review question. The average within- condition variance or MS_error is 1.0. MS_treatment is computed by summing the squared differences between the four condition means and the grand mean and then multiplying by the number of observations per condition. When you treat the factorial design as a one-way design, there are four conditions with three observations per condition. You find there are 105 SS_treatment. With four conditions there are three df_treatment. The resulting MS_treatment is 35. When MS_treatment (35) is divided by MS_error (1.0) you obtain an F-value of 35.0. In each condition there are three observations and, thus, two df. With four conditions there is a total of eight df_error. With three and eight df the critical value found in Appendix F (α = 0.05) is 4.07. Because your obtained F-value (35.0) is greater than the critical value, you will reject the null hypothesis and conclude that there is evidence that treatment condition has an effect.

11.4 The standard error of the mean is obtained by taking the square root of a condition variance divided by the number of observations in that condition: . The standard error of the mean represents an estimate of the standard deviation in the sample means which you would expect to find if you sampled an infinite number of times from the same population (with that particular sample size). The reason that the error bars, which represent the standard errors in the means of each condition, are identical is because the variances and the sample sizes of the four conditions are themselves identical. The variances all equal 1.0 and the sample sizes are all 3.

11.5 The same procedure you used to calculate the simple effects of A at the two levels of factor B can be used to compute the simple effects of factor B at the two levels of A. Again you need to calculate the appropriate, specific GMs. When you are comparing B1 (y̅ =  9) and B2 (y̅ = 7) at A1, the appropriate GM for calculating SS_{Bat A1} is 8.0. When you are comparing B1 (y̅ = 9) and B2 (y̅ = 7) at A1, the appropriate GM for calculating SSBat A2 is 3.0. The SS_error remains the same (8). The df for both the simple effects (1) and error (8) are unchanged.

The resulting observed F(1, 8) = MS_{Bat A1} /MS_error = 6/1 or 6. Because you have a family of two simple effects, you use the critical F-value in the 0.025 table (7.57). Because the observed F-value of 6.0 is less than the critical value, you fail to reject H₀ and conclude there is insufficient evidence to conclude that there is a difference between B1 and B2 at the A1 level.

When you are comparing B1 (y̅ = 5) and B2 (y̅ = 1) at A2 the appropriate GM for calculating SSBat A2 is 3.0. The SS_error remains the same (8). The df for both the simple effects (1) and error (8) are unchanged.

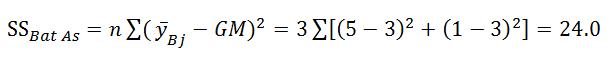
The resulting observed F(1, 8) = MS_{Bat A1} /MS_error = 24/1 or 24. Again, because you have a family of two simple effects, you use the critical F-value in the 0.025 table (7.57). Because the observed F-value of 24.0 is greater than the critical value, you reject H₀ and decide there is sufficient evidence to conclude that there is a difference between B1 and B2 at the A2 level.

11.6 Both eta squared and partial eta squared are standardized effect size statistics. They are both deemed to be an estimate of the amount of variance in the dependent variable accounted for by the treatment variable. A partial eta squared is the sum of squares of the treatment effect divided by the sum of squares for the treatment effect plus the sum-of-squares error for that particular test: SS_treament/(SS_treament + SS_error). This is different from the standard eta squared where the sum of squares for the treatment effect is divided by the sum-of-squares total. When analysing a one-way ANOVA design these two estimates result in the same value. With more complicated designs (e.g., factorial designs) the two estimates will differ. One drawback with reporting a partial eta squared is that in a factorial design their sum can be greater than 100. That is, it can appear that your treatment variables (plus the interaction) account for more than 100% of the variance in your dependent variable. In your current example, the three partial eta squared are 0.938 (bilingual), 0.907 (hourlanglab), and 0.367 (interaction). You would appear to account for 221.2% of the variance in the students’ marks, which is impossible.

11.7 SS_total is identical across the three analyses (233.678): in the factorial design, in the one-way analysis for strategy, and in the one-way analysis for rate. In the one-way analysis SS_strategy (0.311) is unchanged from that found in the factorial analysis. In the other one-way analysis SS_rate (1.558) is also unchanged from that found in the factorial analysis. The df_strategy and the df_rate are also unchanged from those found in the factorial analysis. (The number of treatment conditions for the two independent variables has not changed, thus the degrees of freedom cannot change.) Because SS_strategy and SS_rate as well as df_strategy and df_rate are all unchanged, the corresponding mean squares are unchanged: MS_strategy = 0.311 and MS_rate = 0.779. Their corresponding F-values have changed, however. The F-value for strategy in the factorial analysis was 0.321, whereas in the one-way analysis it is 0.037. The F-value for rate in the factorial analysis was 0.804, whereas in the one-way analysis it is reduced to 0.091. Why have the F-values been reduced? It is the change in their error terms that is responsible for these reductions. SS_error in the factorial analysis used for both strategy and rate was 23.254,  df_error was 24, and MS_error was 0.969. In the one-way analysis of strategy, SS_error was increased to 233.367, df_error was 28, and the resulting MS_error was 8.335. In the one-way analysis of rate, SS_error was 232.120, df_error was 27, and MS_error was 8.597. It is these substantial increases in SS_error in the two one-way analyses that are responsible for their reduced F-values.

Why has SS_error increased in the two one-way analyses? Remember, SS_treatment and SS_total have not changed. Nor has SStreatment -- for the other treatment factor – and nor has SS_interaction changed. Because there is no way in the one-way analysis to identify these two sources of variance, their contribution to SStotal is included in SS_error, the unexplained variance. For example, if you subtract the SS_rate (1.558) and SSinteraction (208.555) from SS_error (233.367) found in the one-way analysis of strategy, you will restore the SS_error (23.254) used in the factorial analysis. Additionally, there are corresponding small differences in the degrees-of-freedom error across the analyses that also influence MS_error.

11.8 The appropriate error term for a set of linear contrasts in a one-way between-subjects design is the error term used in the omnibus test. It remains the best estimate of population variance. Using the variances from all conditions will be more reliable than using only the variances related to the two conditions being compared.

11.9 The average variance would be the average ‘within-condition’ variance, if both factors were between-subjects factors. The average variance also would be the MS_error used to test both the main effects and the interaction in the omnibus ANOVA.

11.10 As more and more of the SS_total are associated with the SS_{between-subjects} the statistical power for the between-subjects factor decreases while the power of the within-subjects factor increases. The treatment sums of squares are not changed, nor the degrees-of-freedom treatment, nor the mean-square treatments. Only the error terms can change. The fewer the SS_total there are associated with the within-subjects side of the analysis, the fewer the SS_error and the smaller the MS_error. Thus, power is increased. This means that more of the SS_total are associated with the between-subjects side of the analysis. The more the SS_total are associated with the between-subjects side of the analysis, the more the SS_error and the larger the MS_error. Thus, power is decreased for the between-subjects factor.