Chapter 5: Testing for a Difference: Two Conditons
Short-answer questions.
1. In a paragraph, describe the logic of a repeated-measures t-test (related samples). For the purpose of constructing the “sampling distribution of the difference between means,” which variance is used? What is the null hypothesis?
Main Points:
- In a repeated measures t-test we examine the difference scores (d-score), which represent the difference between each subject’s scores in the two experimental conditions. If the scores are random with respect to the two conditions, e.g., there is no treatment effect, you would expect roughly an equal number of positive and negative d-scores. More accurately, you would expect the total values of the negative and positive d-scores to be equal. If there is no treatment effect, the Expected Value of the mean d-score is 0.0. If the H1 is correct, the two condition means are estimating two different population means and the expected value of the mean d-score will be non-zero.
- Variance of d-score is used.
- H0 is that the average d-score will be 0, such that any difference in the condition means is due solely to error.
2. How does the randomization test differ from the traditional parametric t-test?
Main Points:
- Parametric t-tests are based on estimates of population parameters, such as means and variances, and thus require assumptions about the shape of underlying distribution.
- Randomization test was designed to calculate the probability of randomness, and is free from any assumptions concerning the shape of the underlying distribution.
3. Imagine you have analyzed your data thinking that they were collected using a within-subject (repeated-measures) design. The t-value was non-significant (p . .05). Subsequently you are told the data were collected using a between-subject (independent samples) design. Is there any chance that the findings will be significant after you re-analyze the data with an independent-samples t-test? If no, why not? If yes, under what circumstances?
Main Points:
- No.
- Procedures for a within-subject design remove all of the factors associated with the individual subject which are responsible for making his or her performance different from that of other subjects. All of these individual differences are sources of variance. As a result, within-subject designs have more power.
- (Actually there is a particular circumstance under which power can increase when a within-subject design is (inappropriately) analyzed as a between-subject design. (Degrees-of-freedom will increase. If there are very few individual differences, the sum-of-squares error will increase very little. Thus, power can increase. This is very rare.)
4. What is the difference between the sign test and signed rank test?
Main Points:
- The sign test utilizes only the sign of the d-scores.
- The Signed Rank Test uses both the sign and the magnitude.
5. How do we calculate the standard error for a “difference between two means?” What is its use?
Main Points:
- Our estimate of the standard error of the difference between two means is made using the Variance Sum Law.
- The Variance Sum Law states that the variance in the difference between (or a sum of) two independent variables is estimated by the sum of the variances of the two variables.
6. Why is a mean d-score the expected value used in the null hypothesis for a repeated measures t-test?
Main Points:
- A positive d-score means that a subject scored higher in condition 1 than he or she scored in condition 2.
- A negative d-score indicates the opposite. If there is no treatment effect, you would expect roughly an equal number of positive and negative d-scores.
- If there is no treatment effect, the Expected Value of the mean d-score is 0.0. Thus, our H0 is that the average d-score will be 0.0.
Data set questions.
1. You want to know whether people are able to identify emotions correctly when we are extremely tired. We know that in the general population (who are not tired), accuracy ratings are on average 82% with a variance of 20. In the present study however, you test 50 people after they participate in strenuous cardiovascular exercise for 45 minutes. You find a mean of 78%. What is the most appropriate test? What can you conclude?
- We test a sample mean using a Z-test when we know the population mean & variance.

2. What simple change can you make to the scores in the shaded condition in Table 5.1 so that the resulting t-value will have a p-value less than .05? (The variance in the condition should not be changed.)
- Add a large constant (e.g., 50) to each score in the shaded condition. This increases the mean while keeping variance the same.
3. Professor Pigeon hypothesized that Long Evans rats are smarter than the common Norway brown rats. To test out his idea he randomly selected 10 rats from each of the two populations. He tests the rats on the standard rat intelligence test: a maze. His data are depicted in the table below. The scores indicate the number of days it took a rat to learn the maze. Did Professor Pigeon find sufficient evidence to support his idea? Include descriptive statistics, tests of assumptions and outliers, an appropriate graph, 95% confidence intervals, and standard effect size estimate, if necessary.


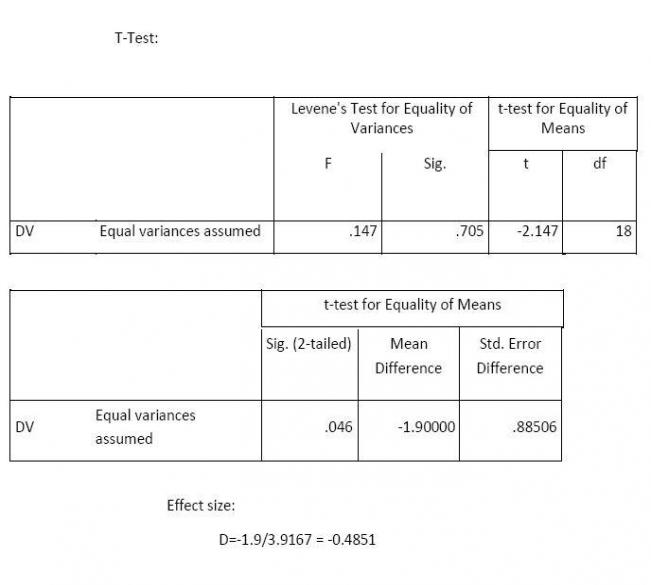
Reject H0. It takes less time for Long-Evans rats to learn the maze in comparison to Brown Norway Rats with a medium effect size.
4. A clinical psychologist wanted to know if a new form of relaxation therapy would reduce the symptoms of her anxious patients. She had her patients report the number of daily symptoms both before and after four weeks of the new therapy. Do the data in the below table provide evidence for the effectiveness of the new form of relaxation therapy?
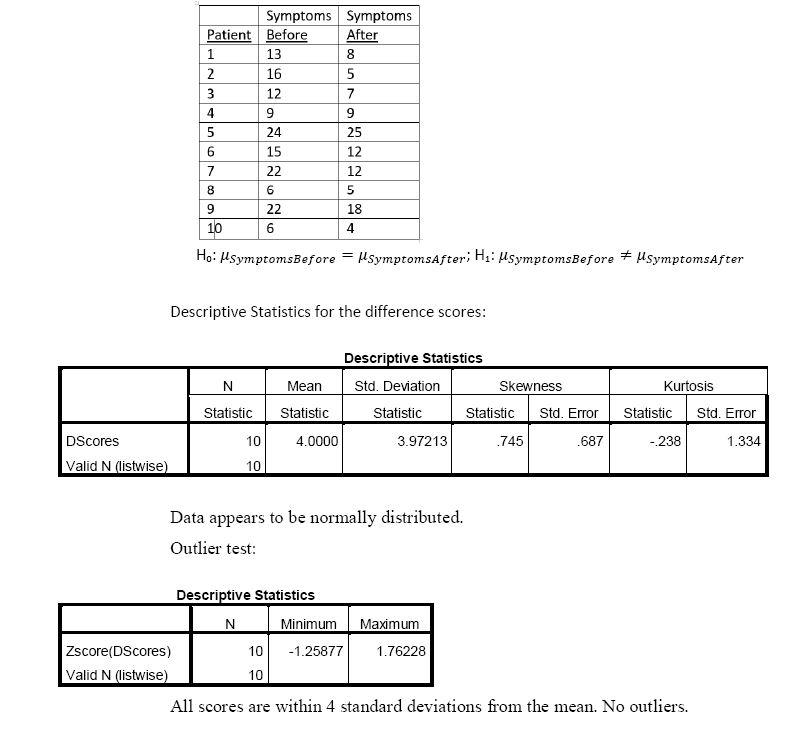
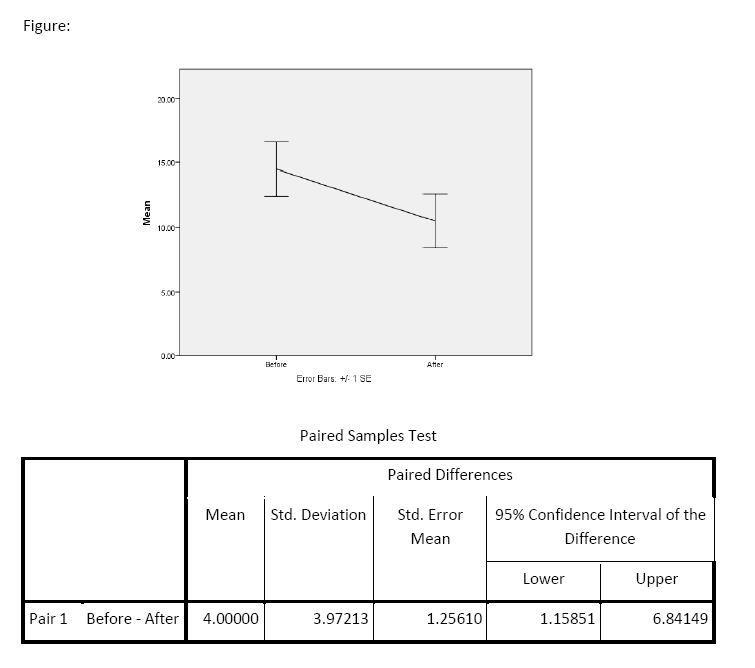

Because she believed anxiety symptoms are not normally distributed, she used a non-parametric test. Do the data in the below table still provide evidence for the effectiveness of the new form of relaxation therapy? What do you think about the normality of the distribution of the symptoms?

