Short answer questions

1. How can a binomial test be transformed into a z-score question?
Main Points:

1. As the number of observations increases the binominal distribution can be treated as a continuous measurement variable, allowing for the conversion to the standard-normal distribution and the inferential use of a z-scores.
   
   1. Determine the value to be converted into a z-score.
   2. Calculate the mean & standard deviation of the binomial distribution. (np and npq)
   3. Convert the determined value into a z-score.

2. What are the limitations to keep in mind when transforming a binomial test into a z-score question?
Main points:

1. When the number of trials is less than 100, the probability associated with the conversion to a z-score problem is different from the probability associated with the binomial approach.
2. The source of the difference resides in the disparity between the smooth distribution of a continuous variable (z distribution) versus the staircase-like distribution of a discrete variable (binomial distribution).

3. What are the three factors that influence power? How do they each influence power?
Main Points:

1. The size of difference between the expected and the observed. The larger the difference between the expected and the observed, the greater the power.
2. The amount of the variance in the DV. The smaller the variance, the greater the power.
3. The number of observations or sample size. An increase in the number of observations (sample size) increases statistical power. 

4. How does the traditional null hypothesis testing approach differ from the randomization approach?
Main Points:

1. The randomization approach highlights the potential distortions associated with assumption of normality necessary for indirectly obtaining a probability from a hypothetical sampling distribution.
2. The randomization test derives the probability of an observed test statistic directly by calculating all possible values of the test statistic by iteratively rearranging the collected data. Thus, an empirical sampling distribution is produced from the researcher’s data.

5. How does the traditional null hypothesis testing (frequentist) approach differ from the Bayesian approach?
Main Points:

1. The central criticism of proponents of the Bayesian approach is that traditional H₀ testing does NOT test the researcher’s H₁. Rather, it tests the probability of the H₀.
2. The Bayesian approach does not involve a H₀. Instead, alternative hypotheses, often referred to as models, are compared. Following the collection of data, the model that “best fits,” in term of probability, is deemed to be the one supported. 

6. What are two problems with using a failure to reject as evidence supporting the null hypothesis?
Main Points:

1. The H₀ is never true.
2. H₀ testing confuses statistical significance with theoretical or practical significance. 

Data Questions

1. Construct a frequency distribution and histogram for 12 tosses of a coin. Assume the probability of a head is .5.

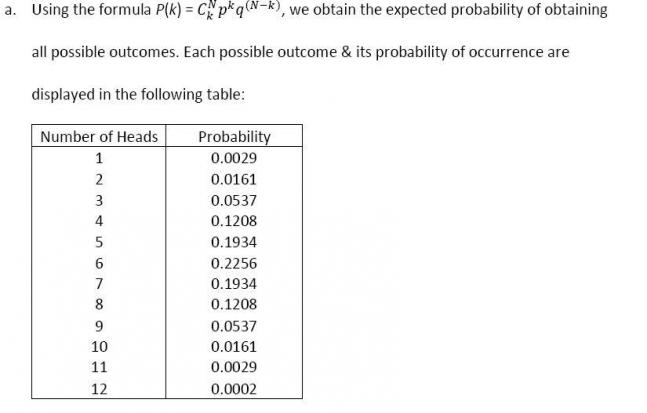
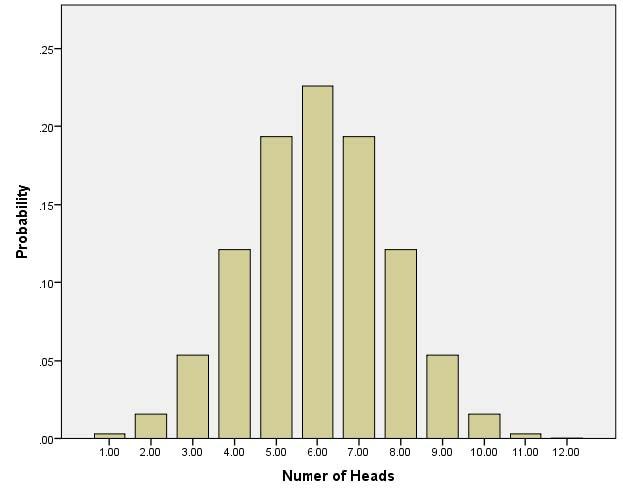
Plot these probabilities using a histogram, where X axis displays the possible outcomes (number of heads from 1 – 12), and y axis displays the expected probability of obtaining each outcome:

2. A drinkologist is interested in consumers’ abilities to differentiate between two brands of a lemon-lime drink. When blindfolded, subjects were asked to taste 14 samples. There were seven samples from each brand randomly presented. A subject correctly identified 11 of the 14 samples.

A. What was the drinkologist’s null hypothesis?

H₀: the subject was guessing; P(Drink1) = P(Drink2) = 0.5

B. If the subject is merely guessing, what is the probability of correctly identifying 11 of the 14 samples correctly?

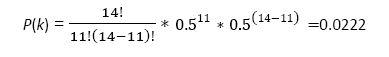
C. Does the drinkologist have sufficient evidence to conclude that the subject was doing anything other than guessing at the brand of the 14 samples?

Yes. The probability of identifying 11 of 14 samples correctly is 2.22%, which is less than 2.5% (two-tailed test). Thus, the drinkologist can reject the null hypothesis

3. Linda was organizing a holiday party for her marketing survey company. In previous years, 40% ate the chicken dish, 40% ate beef, and the remainder ate the vegetarian entrée. She suspects that with all of the new employees, the distribution of preferences will be changed. 100 employees show up for the party: 44 of whom ate the chicken, 44 of whom ate the beef, and only 12 ate the vegetarian entrée.

1. What was Linda’s null hypothesis?

H₀: P(chicken) = 0.4; P(beef) = 0.4; P(Vegetarian) = 0.2;

1. What was Linda’s alternate hypothesis?

1. What are the expected frequencies for chicken, beef, and vegetarian dishes?

E(chicken) = 40; P(beef) = 40; P(Vegetarian) = 20;

1. What is the observed X²value?

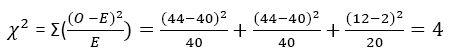
1. What is the critical X² value?

5.991

1. Is there sufficient evidence to support Linda’s suspicion?

No. Linda’s data does not support her suspicion. The distribution of preference this year occurred due to chance.

4. A telecommunications researcher does not believe that two internet providers are equally popular among the local residents. If the researcher determines that the proportional differences between the two providers needs to be at least 70% -30% to be of consequence, how many subjects must the researcher survey to insure power of .8, if the null hypothesis is false? (Assume α= .05.).

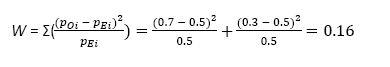
0.16 is a small effect size (Table 1 in Appendix Power). Df = 1.
Number of subjects needed (Table 2 in Appendix Power) is 785.

5. In an infant experiment, a target stimulus and a control are presented randomly on one of two screens (left and right). The baby’s eye movements are tracked. If the infant turns his or her eyes towards the target screen on 18 or more of 20 trials, is there sufficient evidence that the infant can differentiate the target? Use the G-test to answer the question.

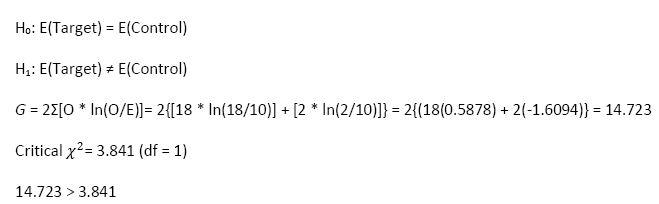
Therefore, we reject the null hypothesis. We have sufficient evidence that the infant can differentiate the target.