Chapter 7: Observational Studies: Two Measurement Variables
Short answer questions
1. What are the two primary distortions associated with the problem of heteroskedasticity?
Main Points:
- The correlation coefficient will underestimate the strength of the association for some segments of the x-axis and will overestimate the association at other segments.
- The amount of error (standard error of the estimate) related to predictions will be underestimated for some segments of the x-axis and will be overestimated at other segments
2. What is the third-variable problem and how is it relevant to correlation and OLS regression analysis?
Main points:
- The third-variable problem highlights the importance for the researcher to not only know the most appropriate statistical test to employ, but also to be able to identify potential third-variable problems and how to eventially control for their effects.
- The third variable is a potential source of concern in OLS regression with respect to the reliability and validity of B and r.
3. Why is linearity a necessary assumption of both correlational and regression analysis?
Main Point:
- Because correlational and regression analysis are concerned only with OLS linear associations.
4. Why is homoskedasticity an assumption of both correlational and regression analysis?
Main Points:
- Violation of homoscedasticity can cause under- or overestimation for both correlational (strength of association) and regression analyses (prediction errors).
- Inconsistency across the regression line is the source of the over and under estinmates.
5. What is the third-variable problem and how does it pertain to correlational analysis?
Main Points:
- The third-variable problem highlights the importance for the researcher to not only know the most appropriate statistical test to employ, but also to be able to identify potential third-variable problems and how to eventially control for their effects.
- Third-variable can present serious problems for interpreting simple correlation studies.
- It can lead to overestimates or underestimates of the correlation.
6. How are the ![]() coefficient and r related? How are they different?
coefficient and r related? How are they different?
Main Points:
- Both
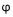 and r are standardized estimates of the strength or degree of association between two variables.
and r are standardized estimates of the strength or degree of association between two variables. - Φ measures association between two categorical (nominal and ordinal) variables, r measures association between two measurement variables.
- The absolute values of both range from 0.0 to 1.0.
Data set questions.
1. The manager of the Toronto United soccer club is interested in the number of matches his starting 11 players missed due to injury. It seemed to him that those who missed more matches than the others one year also missed more matches the next year. To test his suspicion he recorded the number of days the 11 players missed due to injury for two years. The data are reported in the below table. It lists the number of days each of the players missed during the two years. Do the data support the manager’s suspicion? Be sure to create a scatterplot and any necessary test of significance.
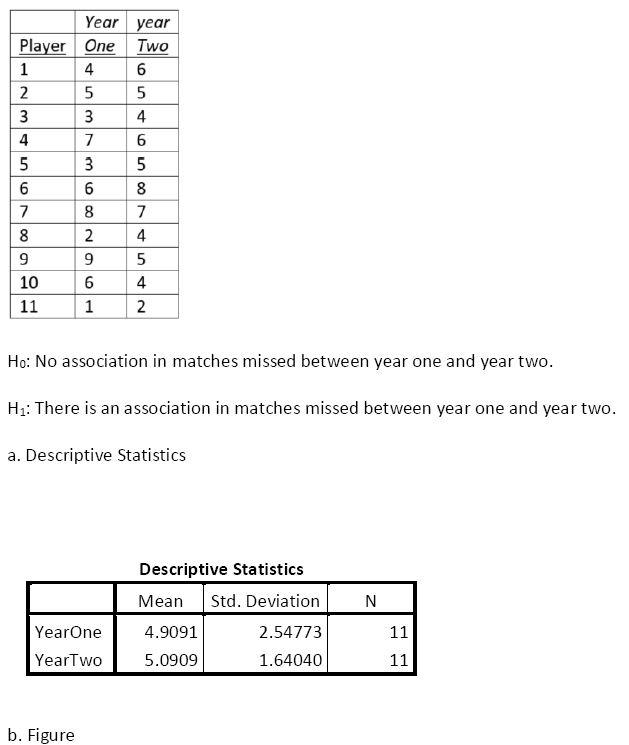
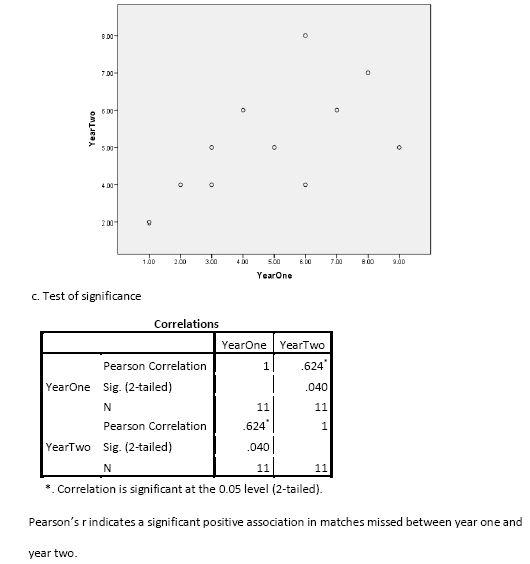
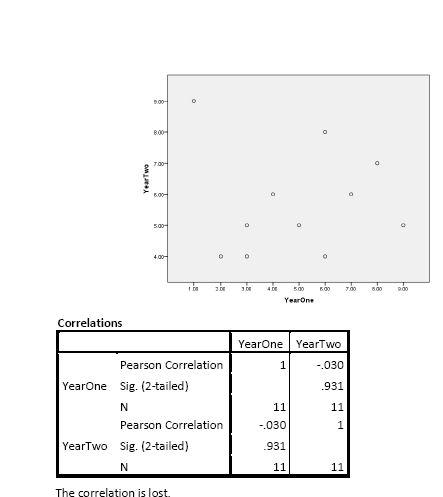
2. How would the results change if Player #11’s number of missed matches in Year Two changed from 2 to 9?
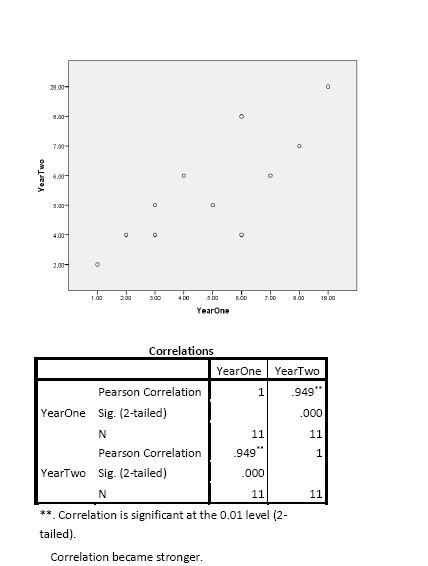
3. How would the results change if Player #9 had missed 19 matches in Year One and 28 matches in Year Two? (Return Player # 11’s Year Two number of missed matches to 2.)
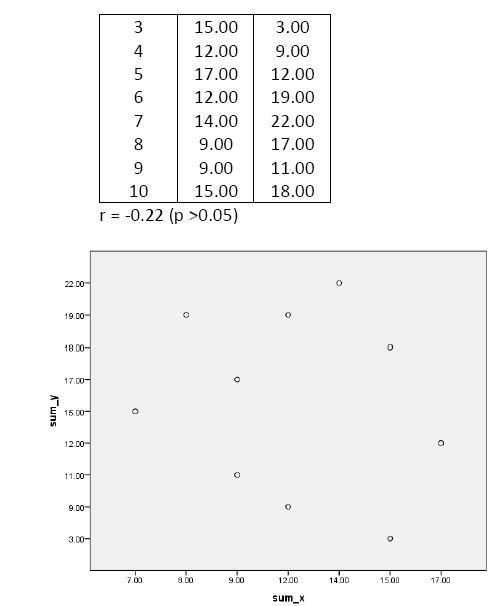
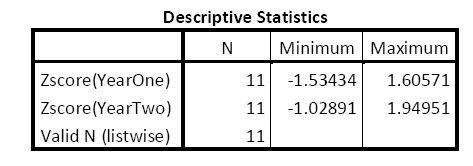
4. Are there any univariate or bivariate outliers in the data used in Questions #2 and #3?
Main notes: outliers are defined as scores 4 standard deviations above or below the mean.
a. Univariate outlier check:
Question2:
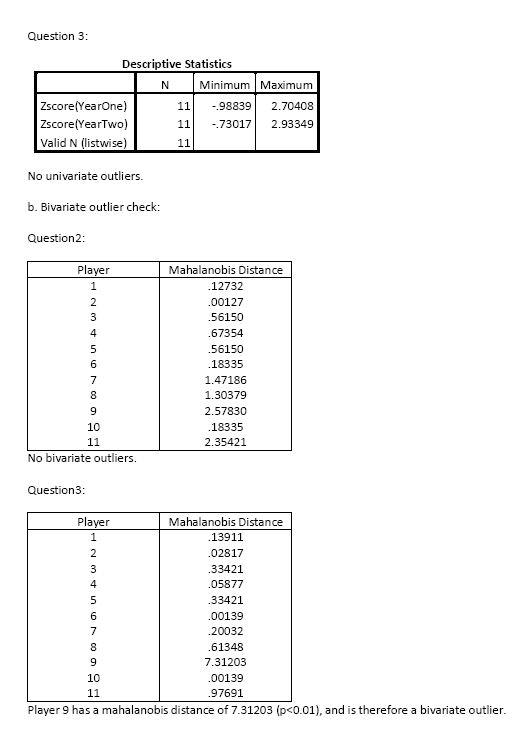
5. What do Questions #2 and #3 illustrate?
- Questions 2 & 3 illustrate the necessity of inspecting scatterplots prior to judging and reporting correlation coefficients.
- Question 3 illustrates the distortion effect of a bivariate outlier.
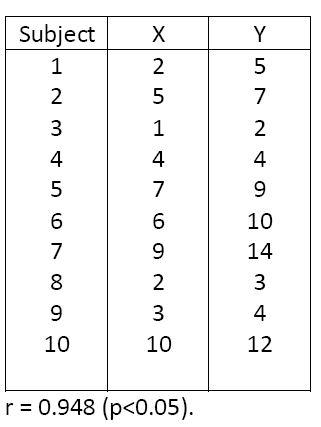
6. A cultural anthropologist suspected that those who watched more home renovation programs on television would also be those who watched more cooking programs. To test out her hypothesis she asked ten of her neighbours to keep track of the number of home renovation and cooking programs they watched for a week. The data are reported in the below table.
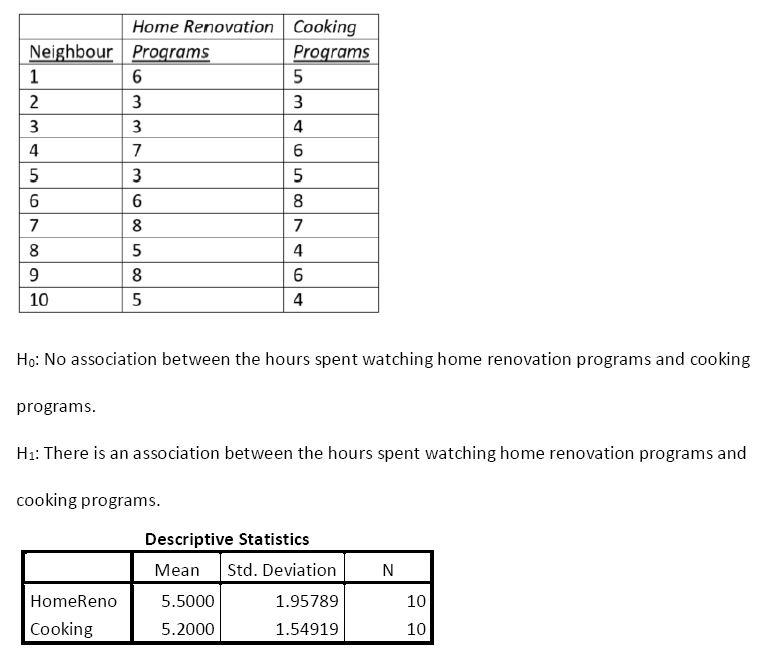
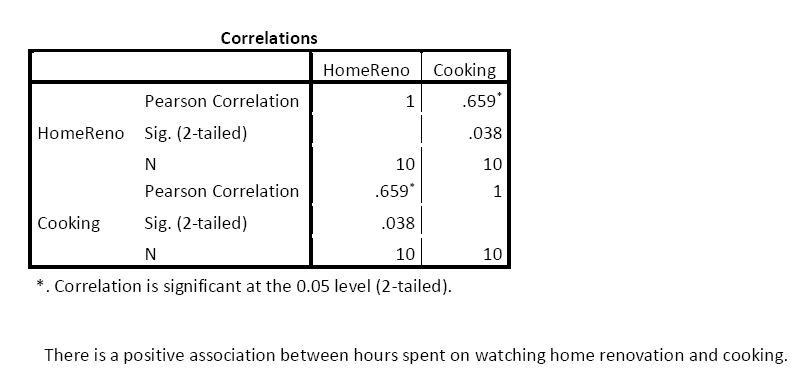
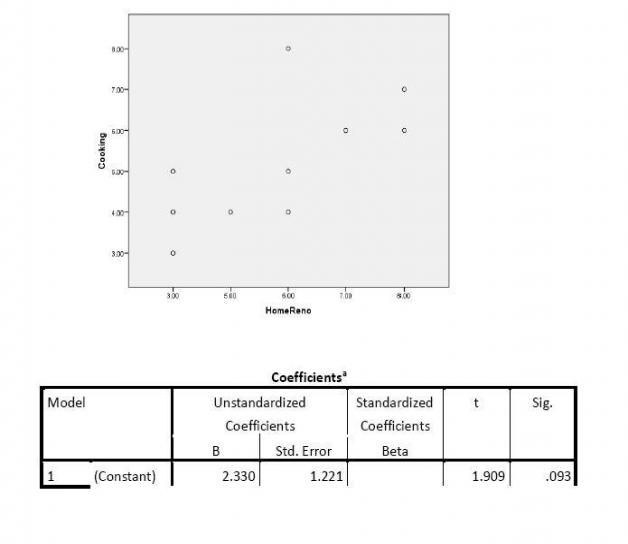
7. If another neighbour watched 4 hours of home renovation programs during a week, how many hours would you predict this neighbour would watch cooking programs? Include in your answer a scatterplot and any necessary tests of significance.
Coefficientsa Model Unstandardized Coefficients

8. Create two data sets where the correlation coefficients are significant. When the two data sets are amalgamated, however, the resulting correlation coefficient should be non-significant. Use ten subjects in each of the data sets. The x and y variables should be the same in both of the original data sets.