Short answer questions.

1. How do the rational and empirical approaches to probability differ?
Main Points:

1. The rational approach raises reasoning and logic to the level of mathematical precision, and refers to knowledge that is rational or logical in nature, rather than empirical (based on experience).
2. The empirical approach produces probabilities based on what is observed.

2. What is the “asymptotic trend”?
Main Point:

1. The asymptotic trend states that as you increase the number of observed outcomes the difference between the expected frequencies (rational in nature) and the observed frequencies (empirical in nature) of the outcomes becomes progressively smaller.

3. How is the ceiling effect related to skewness?
Main Point:

1. Ceiling effect refers to when data are clustered at the top of the range. Data that displays a ceiling effect has a distribution that is positively skewed.
2. The test does not allow for differentiation at the top of the distribution.

4. Why is it important to identify outliers?
Main Point:

1. Outliers can create skewness.
2. The can distort the mean and variance.

5. In a deck of playing cards, are hearts and queens mutually exclusive? Why?
Main Points:

1. Hearts and queens are not mutually exclusive.
2. Two events are mutually exclusive if the occurrence of one event precludes the occurrence of the other. Queen of hearts has both possible outcomes simultaneously.

6. What is the additive law of probability? How is it related to assumption of mutual exclusivity?
Main Point:

1. The additive law of probability states that if two events are mutually exclusive then the probability of one of the two events occurring is the sum of their individual probabilities.

7. How does a medical test’s sensitivity and specificity influence the likelihood that a patient will have the disorder for which he or she was tested, if he or she tests positive?
Main Points:

1. Sensitivity is the probability of testing positive when the patient has the disease. Higher sensitivity decreases the likelihood of false negatives.
2. Specificity is the probability of testing positive when the patient does not have the disease. Lower specificity decreases the likelihood of false positives.

8. Imagine creating a frequency histogram from a very large set of observations. Now imagine transforming those observations into z-scores and creating another frequency histogram. How will the two histograms compare with each other?
Main Point:

1. The histograms will appear to have the same distribution. However, the histogram from the set of observations will have its own mean and standard deviation, whereas the histograms from z-scores will always have a mean of 0 and a standard deviation of 1.

Data set questions

1. In the following table, are height (tall or short) and choice of beverage (coffee or tea) independent? Why?

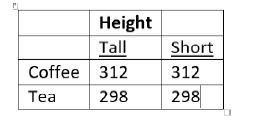
Given the table, a person’s height and his/her choice of beverage are independent. Knowing a person’s height does not alter the probability of his/her beverage choice.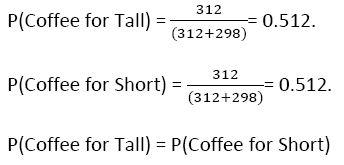

2. Using the table found in question #1, what is the probability of being tall and preferring tea?

3. In the following table, are height (tall or short) and choice of beverage (coffee or tea) independent? Why?

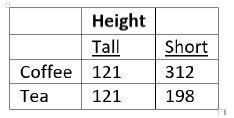
Given the table, a person’s height and his/her choice of beverage are not independent. Knowing a person’s height alters the probability of his/her beverage choice.

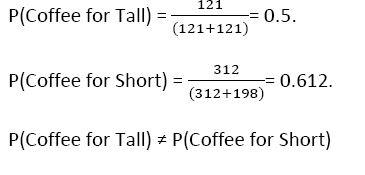
4. If the probability of a basketball player making a free-throw is .5, what is the probability of the player making 9 out of 10 free-throws?

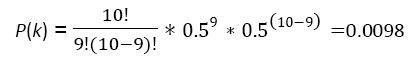
5. If the probability of a basketball player making a free-throw is .8, what is the probability of the player making 9 out of 10 free-throws?

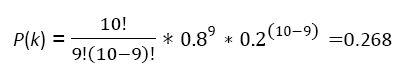
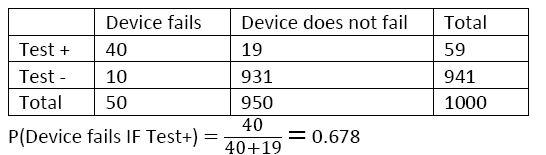
6. Your car dealer has informed you that her computer assessment of your car indicates that your emission control device is about to fail. Assume this device only fails in about 5% of all cars. The dealer further informs you that in those cases where the emission control device fails, the computer would correctly identify the problem 80% of the time.
Furthermore, her computer indicates a problem in only 2% of the cars when there is no problem with the emission device. What is the probability that your car’s emission control device will shortly fail?

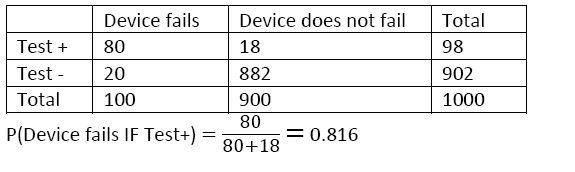
7. If we assume the emission control device in question #6 fails in about 10% of all cars, what is the probability that your car’s device will shorty fail?

9. If a population has a mean of 60 and a variance of 81, within what two scores will 95% of the observations fall?

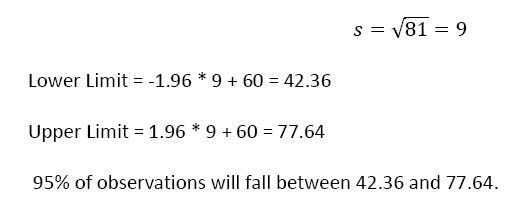
10. An instructor who teaches introductory level Italian has found over the years that students in her classes spend on average 28 minutes a week practicing in the language lab. She also knows that the standard deviation is 5 minutes per week. She looks at the log book for the lab and finds a student who spent 38 minutes in the lab this week. Does she have evidence that this student comes from a different “population” than the other students who are in her course? On what basis can she draw the conclusion? What limitation should she place on her conclusion?

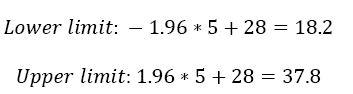
Due to chance alone, with 95% confidence, time spent in lab within the population may be anywhere between 18.2 and 37.8 minutes. Because the student spent more time than the upper limit, the instructor can reject the hypothesis that the student is a member of the population.
Limitation the instructor should place on her conclusion is the possibility of a Type-I error. That is, there is a 5% chance she has incorrectly rejected her hypothesis.