Chapter 6: Observational Studies: Two Categorical Variables
Short-answer questions.
1. What is the difference between a X2 goodness-of-fit and a X2 test-of-independence?
Main Points:
- In a X2 test-of-independence there is an addition to the logic behind deriving the expected frequencies based on the assumption of independence and the multiplicative law of probability.
- There is one model to test: independence.
2. How are the expected frequencies for the X2 test-of-independence derived?
Main Points:
- The expected frequencies are produced based on the assumption of independence and the multiplicative law of probability.
- For a 2x2 contingency table, assuming independence and using the multiplicative law of probability, we can obtain the probability of each cell in the contingency table as: P (A & B) = p(A) * p(B)
- Then, the expected frequencies for the four cells can be obtained by multiplying the probabilities of the four cells by the total number of observations
3. Why is the coefficient an inappropriate measure of strength of association for a contingency table with more than two rows and columns?
Main Point:
- Once the contingency table contains more than two rows or columns,
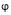 can exceed 1.0.
can exceed 1.0. - Thus the results overestimate the strength of association.
4. What is the third-variable problem and how might it be addressed?
Main Points:
- The third-variable problem is a type of confounding.
- The third variable must be held constant or controlled in some way.
- It highlights the importance for the researcher to know the most appropriate statistical test to employ, to understand the phenomenon under investigation, and to be familiar with the relevant literature.
5. What is a limitation of lambda as a measure of the strength of an ordinal association?
Main Point:
- Lambda is used for nominal data.
Data set questions:
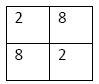
1. If an observed X2 value was 7.20 (df = 1, p = .007) and all of the expected frequencies were 5, what were the observed frequencies in the four cells?
Given 1 degree of freedom and four cells, we have a 2x2 contingency table, and thus a test of independence. To get a X2 of 7.2, the sum of squared difference between the observed and expected frequencies needs to be 36, and the sum of expected frequencies needs to be equal to the sum of observed frequencies for each row and column. A possible set of values is:
2. Marco d’Naldo was reading about the caloric differences between standard ice cream and gelato. He wondered if the choice of ice cream versus gelato is related to whether the person is on a diet. One day Marco goes to an ice cream parlour (which also serves gelato) and surveys the customers. His data are summarized in the below contingency table.
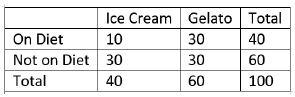
A. What is the null hypothesis?
H0: Ice cream choice and diet are unrelated.
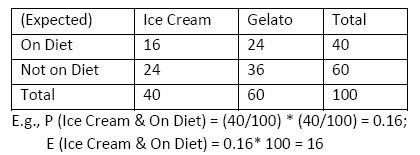
B. What are the expected frequencies?
C. What is the observed X2 value?
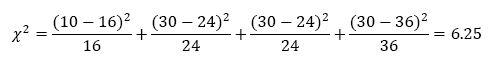
D. How many degrees-of-freedom are there?
df = (2-1) * (2-1) = 1
E. What is the critical X2 value?
3.84
F. Would Marco d’Naldo reject the null hypothesis?
Yes
G. What is the effect size?
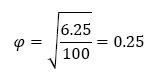
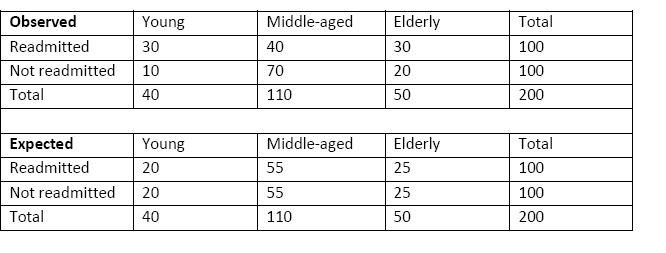
3. Dr. Head, a clinical psychologist, claims that the recidivism rate (the likelihood that a patient will be readmitted) for a given psychological disorder is unrelated to age group (young, middle-aged, and elderly). To answer his question he randomly checked the files of three age categories: 40 young patients, 110 middle-aged patients, and 50 elderly patients who had had the disorder. Of these patients, the total number of patients who had been readmitted to the hospital with their disorder was 100. Of these 30 were young and 40 were middle-aged.
- Do the clinician’s findings support his claim?
H0: Recidivism rate & age group are unrelated.
H1: Recidivism rate & age group are related.

4. Create two data sets for 2X2 contingency tables. Both of the data sets should produce a significant X2 test-of-independence. When the two data sets are amalgamated, however, the X2 test-of-independence for the combined data set should be non-significant.
- Create 2 separate tables:

