13.4 A communality is the amount of variance in an original variable accounted for by the retained factors. There is only one way that all of the original variables can have communalities of 1.0 and that is for all of the original variables to be completely uncorrelated with each other. In such a case the correlations among the original variables would all be 0.0 and each variable would load perfectly on its own factor. All factors would have eigenvalues of 1.0.

13.5 The proportion of the total variance associated with an eigenvalue is based on the number of variables analysed. An eigenvalue is the percentage of the total variance the average variable in the data set accounts for divided by the percentage of the variance for which the derived factor accounts: 

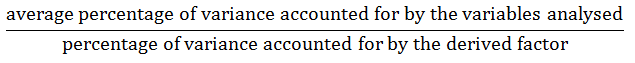
or

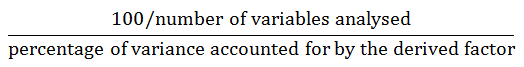
If there are only four variables in the PCA, on average each of the variables is associated with 25% of the total variance. If a derived factor accounts for 50% of the total variance, then that factor has an eigenvalue of 2.0. If a derived factor accounts for 25% of the total variance, then that factor has an eigenvalue of (25/25) 1.0. If a derived factor accounts for 35% of the total variance, then that factor has an eigenvalue of (35/25) 1.28. Because you have 16 TAI variables in the analysis, the average variable accounts for (100/16) 6.25% of the total variance. A derived factor that accounts for 6.25% of the variance would have an eigenvalue of 1.0. Any derived factor with an eigenvalue less than 1.0 would necessarily account for less than 6.25 % of the variance. For example, a derived factor with an eigenvalue of0 .5 would be associated with only [0.5(6.25)] 3.125% of the total variance.

13.6 The two-component model resulting from using an eigenvalue of 1.0 as the cut-off accounted for 53.350% of the variance. The forced four-component model accounted for 64.174% of the total variance. The component loadings on the first two factors are identical across the two PCAs. The loading of the 16 variables on components 3 and 4, which resulted from the forced four-factor model, in general are weaker relative to their corresponding loading on components 1 and 2. This is necessarily the case because components 3 and 4 account for much less of the total variance than that accounted for by factors 1 and 2. Keep in mind that the component loadings are correlations between the variable and the derived component or factor. 

13.7 Return to the Factor Analysis Extraction window and select the Fixed number of factors option and then indicate the number of factors you wish to extract. Then rerun the PCA and systematically increase the number of factors to be retained. You will find that you will not account for 80% of the total variance until you retain nine factors (81.166%). The component loadings on these additional factors are very small, indicating that the derived factors explain very little of the variance in the variables. Stated the other way around, the variables contribute very little to these additional components or factors.