Short answer questions.

1. With a one-way, between-subject design why is the Expected Value of the F-ratio equal to 1.0, if the null hypothesis is true?
Main points:

1. The denominator (Mean-Square Error) is always an unbiased estimator of the population variance.
2. If the null hypothesis is true, the numerator (Mean-Square Treatment) is also an unbiased estimator of the population variance.
3. Because the Expected Value of both are the same, the ratio is necessarily 1.0.

2. On average, what happens to the F-ratio if the null hypothesis is false? Why?
Main Points:

1. When the null hypothesis is false, it means that there is a treatment effect
2. The denominator (Mean-Square Error) is always an unbiased estimator of the population variance.

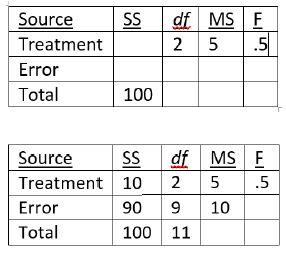
4. Complete the missing value in the below ANOVA summary table.

 

5. Given the following descriptive statistics, what is the resulting F-value?

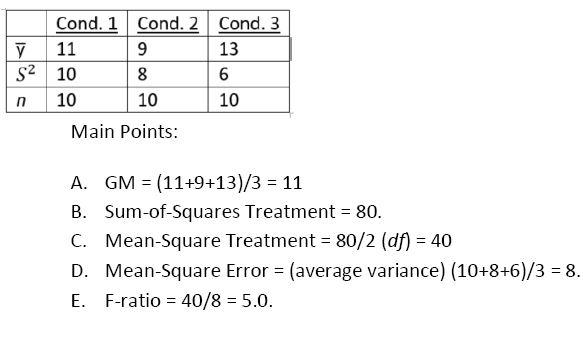
Data set questions.

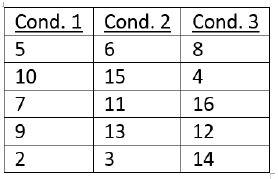
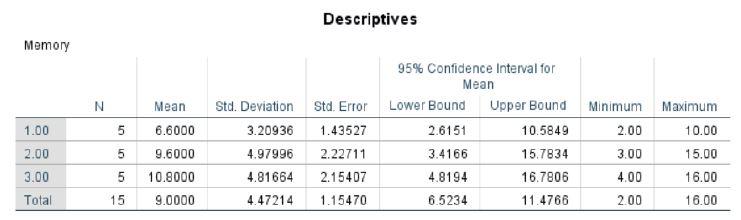
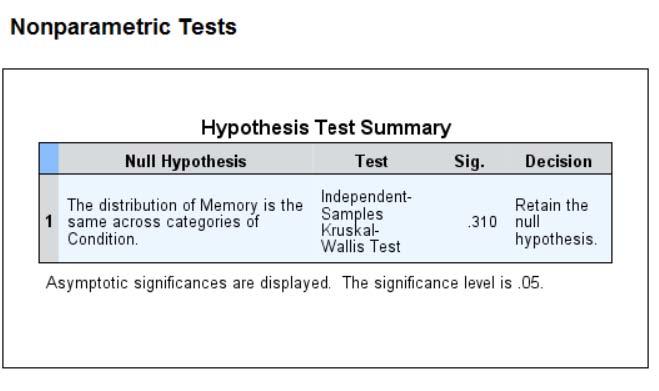
1. A psychologist hypothesized that meditation prior to a memory test would improve scores. To test her hypothesis, she randomly assigned 15 subjects to 3 conditions: condition 1 (no meditation), condition 2 (5 minutes of meditation), and condition 3 (10 minutes of meditation). Do the below data support her hypothesis? The scores are the number of items correctly recalled. Be sure to include all tests of assumptions (with conclusions), descriptive statistics, an appropriate graph, ANOVA summary table, and state and test the overall null hypothesis. Complete the analysis two ways: first assuming that you can make the parametric assumptions, and second assuming that you cannot make those assumptions. Draw the appropriate conclusions from both analyses.

Main Points:
A. The descriptive statistics allow you to test for outliers (4 X standard deviation).

B. The bar graph indicates that there is a trend consistent with the researcher’s hypothesis.

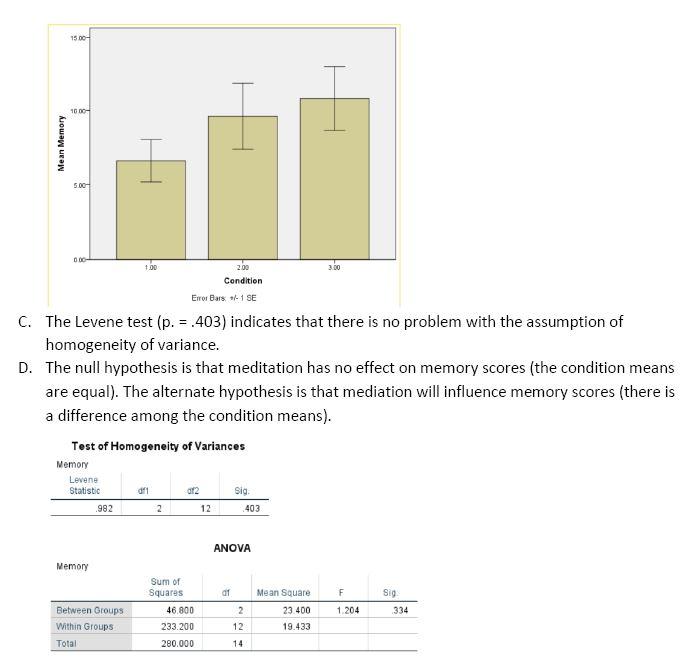
E. There is insufficient evidence to reject the null hypothesis: F = 1.204, MSE = 23.4, p. = .334. Thus, there is insufficient evidence to support the researcher’s hypothesis. There could be a problem with insufficient power. This could represent a Type II error.
F. The non-parametric Kruskal-Wallis test results in the same outcome.

2. First, imagine an analysis where the Sum-of-squares total, treatment, and error are 73.6, 19.6, and 54, respectively. The degrees-of-freedom are 14, 2, and 12 respectively. Assuming a between-subject design, what is the resulting F-value and what do you conclude? Now imagine a covariate that accounts for 50% of the sum-of-squares total. What is the new resulting F-value and what do you conclude?
Main points:

1. Mean-Square Treatment = (19.6/ 2) = 9.8
2. Mean-Square Error = (54/12) = 4.5.
3. F value = (9.8/4.5) = 2.18. Critical F-value = 3.89.
4. We fail to reject the null hypothesis and conclude that there is insufficient evidence that the independent variable influence the dependent variable.
5. New Sum-of-Squares Total is 73.6(.5) = 36.8.
6. New Sum-of-Squares Error is 36.8 – 19.6 (sum-of-squares treatment) = 17.2.
7. New degrees-of-freedom error is 11
8. New Mean-Square Error is 17.2/11 = 1.56.
9. The new F value is (9.8/1.56) = 6.28.
10. Reject the null hypothesis (critical F-value = 3.98). There is sufficient evidence to conclude that the independent variable influences the dependent variable.

3. Construct a data set of 15 whole numbers between 5 and 20. Separate them into three equal groups (treatment conditions) twice, once where the resulting F-ratio would be significant and once where the resulting F ratio would not be significant. Try to keep the within group variances as similar as possible across all SIX groups.
Main Points:

1. Condition variances and the variability among condition means are independent. This is the basis for the two estimates of population variance that comprise the F-ratio.
2. The strategy is to group the numbers in two ways:
   1. Once where the means are relatively close together.
   2. Once where the means are far enough apart to produce a significant F-ratio.