Statistics with R
Student Resources
Chapter 10: Hypothesis Tests About u and p: Applications
1. Referring to the Agrico example (Section 10.1), suppose the quality-control manager decides that while Agrico does not want to underfill its packages, neither does it wish to overfill. Clearly, giving away product in overfilled packages costs Agrico money, and provides little or no goodwill among customers who are unaware they are reaping a windfall in free bran flakes. Suppose that the sample size is adjusted upward to n = 100 and α is reset to 0.10. Using the six-step hypothesis-testing framework, test H0 : µ 375 against Ha : µ>375. Recall that σ = 22.5. Suppose the sample of n = 100 provides a mean weight of 377.50 grams. What is the p-value?
Answer: p-value = 0.1333.
(a) H0 : µ ≤ 375
(b) Ha : µ>375
(c) n = 100 and α = 0.10
(d) Reject H0 : µ ≤ 375 if z>zα = z0.10 = 1.282. That is,
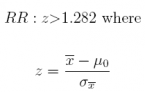
qnorm(0.90)
## [1] 1.281552
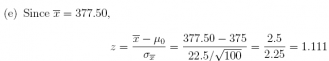
(f) Since z = 1.111<1.282 (and thus does not fall in the RR), we do not reject H0. We cannot conclude from the evidence that Agrico is overfilling its packages.
The p-value = p(z>1:111) = 0.1333.
pnorm(1.111, lower.tail = FALSE)
## [1] 0.1332842
Since p-value = 0.1333> = 0.10, we do not reject H0.
2. Family physicians in Tampa, Florida reportedly earn an average annual salary of $141, 300. Suppose we conduct a survey on a sample of n = 64 family physicians from New Orleans, Louisiana to test whether their mean annual salary is different from the reported mean in Tampa, and nd that the sample mean is $138, 000. Assume = $18, 000. At the level of α = 0.01, use the six-step framework to test
H0 : µ = 141. 300 against ![]() What is the p-value?
What is the p-value?
Answer: p-value
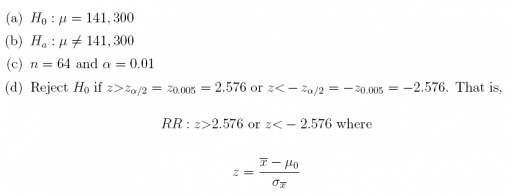
qnorm(0.005)
## [1] -2.575829
qnorm(0.995)
## [1] 2.575829
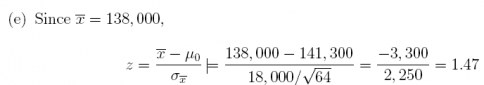
(f) Since z = 1.47<2.576 (and thus does not fall in the RR), we do not reject H0. We cannot conclude from the evidence that the mean salary among New Orleans physicians is different from that of Tampa physicians.
The p-value = (2)(p(z>1.47)) = 0.1416.
2 * pnorm(1.47, lower.tail = FALSE)
## [1] 0.1415618
Since p-value = 0:1416> α= 0.01, we do not reject H0.
3. The student newspaper at a large business school claims that 55% of graduating students have an offer of employment even before they graduate. The Office of Student Affairs decided to investigate this claim to see whether it is true. When they carried out the survey, they found that 321 of 535 graduating students reported having a job offer. At a level of α = 0.10, use the six-step framework to test H0 : p = 0.55 against ![]() What is the p-value?
What is the p-value?
Answer: p-value = 0.02034
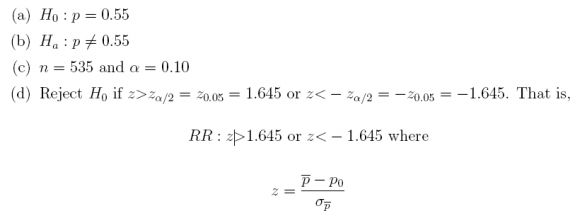
qnorm(0.05)
## [1] -1.644854
qnorm(0.95)
## [1] 1.644854
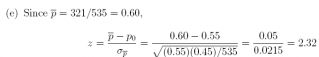
(f) Since z = 2.32>1.645, we reject H0 and conclude that the percent of students having jobs upon graduation differs from (and exceeds) 0.55
The p-value = (2)(p(z>2.32)) = 0:02034.
2 * pnorm(2.32, lower.tail = FALSE)
## [1] 0.02034088
Since p-value = 0.02034< = 0.10, we reject H0.
Alternatively, we may use the prop.test() function, making sure that we specify the ve arguments as follows. Note that the positive square root of X-squared = 5.4 (see the fourth line below) is 2.32, which equals the z test statistic above.
prop.test(321, 535, p = 0.55, conf.level = 0.90, correct = FALSE)
##
## 1-sample proportions test without continuity correction
##
## data: 321 out of 535, null probability 0.55
## X-squared = 5.404, df = 1, p-value = 0.02009
## alternative hypothesis: true p is not equal to 0.55
## 90 percent confidence interval:
## 0.5647427 0.6342509
## sample estimates:
## p
## 0.6
4. While campaigning for higher political oce during a recent election, a certain candidate claimed that "At least 75% of voters want the country to end all foreign aid to all countries." When a polling organization conducted a survey to investigate this claim, they found that 242 out of a sample of n = 346 expressed agreement with the statement. At a level of α = 0.02, use the six-step framework to test H0 : p ≥ 0.75 against Ha : p<0.75. What is the p-value?
Answer: p-value = 0.0149.
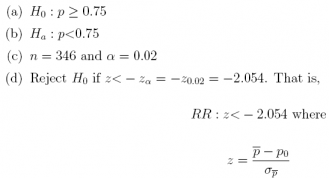
qnorm(0.02)
## [1] -2.053749
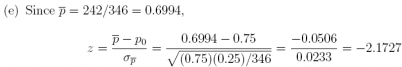
(f) Since z = –2.1727<– 2.054, we reject H0 and conclude that the proportion of people favoring elimination of foreign aid is less than 0.75.
The p-value = p(z< – 2.1727) = 0:0149.
pnorm(-2.1727)
## [1] 0.01490145
Since p-value = 0.0149< α = 0.02, we reject H0.
Alternatively, we may use the prop.test() function.
prop.test(242, 346, p = 0.75, conf.level = 0.98, alternative ='l',correct = FALSE)
##
## 1-sample proportions test without continuity correction
##
## data: 242 out of 346, null probability 0.75
## X-squared = 4.7206, df = 1, p-value = 0.0149
## alternative hypothesis: true p is less than 0.75
## 98 percent confidence interval:
## 0.0000000 0.7473958
## sample estimates:
## p
## 0.699422
5. An Italian farmer who grows and packs agricultural produce for the export market claims that his packages contain an average of 750 grams of tomatoes. To ensure that the company consistently meets this standard, the manager conducts a study to test H0 : µ≥ 750 against Ha :µ <750. Based on previous studies, σ = 25. What sample size should the manager use if he wants a 0.90 probability of identifying
when the mean weight falls short of 750 grams by 10 grams? Let α = 0.01.
Answer:
![]()
qnorm(0.01, lower.tail = FALSE)
## [1] 2.326348
qnorm(0.10, lower.tail = FALSE)
## [1] 1.281552
