Statistics with R
Student Resources
Chapter 2: Descriptive Statistics: Tabular and Graphical Methods
1. A marketing research survey of 1,095 households investigating attitudes toward the following brands—A, B, C, D, E and F—in a certain product category reveals the following brand preference structure: 272 prefer brand A, 212 prefer brand B, 297 prefer C, 38 prefer D, 181 E, and 95 F. Create an object, named E2_1, which contains this information, and then provide the frequency disribution of preferences across the six brands.
Answer:
#Comment1. Use the rep() function to produce the data values and
#read data into object named E2_1.
E2_1 <- c(rep('A', 272), rep('B', 212), rep('C', 297), rep('D', 38), rep('E', 181), rep('F', 95))
#Comment2. Use the table() function to produce a frequency
#distribution and read the result into object named fd.
fd <- table(E2_1)
#Comment3. Examine contents of fd.
fd
## E2_1
## A B C D E F
## 272 212 297 38 181 95
Thus the table() function provides the frequency distribution across the six brands.
2. Create the relative frequency distribution of brand preference. Use the E2_1 data.
Answer:
#Comment1. Use the table() function to produce a frequency
#distribution and read the result into object named fd.
fd <- table(E2_1)
#Comment2. Create relative frequencies and assign to object rf.
rf <- fd / sum(fd)
#Comment3. Examine contents of rf.
rf
## E2_1
## A B C D E F
## 0.24840183 0.19360731 0.27123288 0.03470320 0.16529680 0.08675799
The relative frequency distribution of brand preference: A is 0.25, B is 0.19, C is 0.27, D is 0.03, E is 0.17, and F is 0.09.
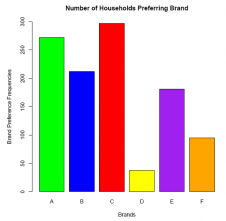
3. Show the bar graph of brand preference frequencies. Set the range of the vertical axis from 0 to 300. Define the colors of the bars, from left to right, as green, blue, red, yellow, purple, and orange. Provide a label for both horizontal and vertical axes as well as a main title for the picture. Use the E2_1 data.
Answer:
#Comment1. Use the table() function to produce a frequency
#distribution and read the result into object named fd.
fd <- table(E2_1)
#Comment2. Use the barplot() function to provide a bar graph.
barplot(fd,
col = c('green', 'blue', 'red', 'yellow', 'purple','orange'),
ylim = c(0, 300),
main ='Number of Households Preferring Brand',
xlab ='Brands',
ylab = 'Brand Preference Frequencies' )
We have listed the arguments vertically (for the barplot() function), one per line, for the sake of minimizing clutter and improving visual clarity. In practice, however, there is no need to do so, and we can just as easily write the entire function (with its six arguments) on one line.
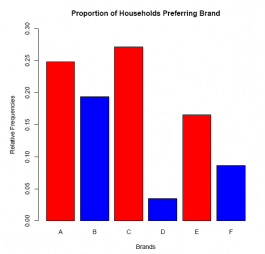
4. Show the bar graph of brand preference relative frequencies. Set the range of the vertical axis from 0 to 0.30. Define the colors of the bars, from left to right, as red, blue, red, blue, red, and blue. Provide a label for both horizontal and vertical axes as well as a main title for the picture. Use the E2_1 data.
Answer:
#Comment1. Use the table() function to produce a frequency
#distribution and read the result into object named fd.
fd <- table(E2_1)
#Comment2. Create relative frequencies and assign to object rf.
rf <- fd / sum(fd)
#Comment3. Use the barplot() function to produce bar graph.
barplot(rf,
col = c('red', 'blue', 'red', 'blue', 'red', 'blue'),
ylim = c(0, 0.30),
xlab ='Brands',
ylab ='Relative Frequencies',
main = 'Proportion of Households Preferring Brand')
5. Show the dot plot of the relative frequency of brand preferences. Use the E2_1 data.
Answer:
#Comment1. Use the table() function to produce a frequency
#distribution and read the result into object named fd.
fd <- table(E2_1)
#Comment2. Create relative frequencies and assign to object rf.
rf <- fd / sum(fd)
#Comment3. Use the dotchart() function to create a dot plot.
dotchart(sort(rf),
xlab ='Relative Frequencies Brand is Preferred',
main ='Relative Frequencies by Brand',
pch = 20,
col ='blue')
## Warning in dotchart(sort(rf), xlab = "Relative Frequencies Brand is Preferred", : 'x' is neither a vector nor a matrix: using as.numeric(x)
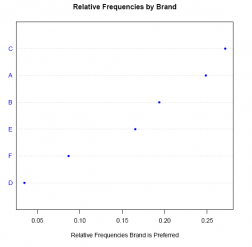
Note: it is necessary to sort the relative frequency data if we want the points in the dot plot to run in sequential order from the lower-left to the upper-right. This is done by nesting the sort() function as an argument in the dotchart() function. If we omit the sort() function, and include only the object name (in this case rf), the points in the plot are ordered alphabetically by default.
Note: This routine provides a warning message that we are free to ignore because the dotchart() function executes successfully and produces the dot plot image.
6. Develop a frequency distribution of these values: 24, 29, 34, 29, 37, 26, 30, 34, 30, 11, 12, 14, 18, 38, 17, 13, 16, 12, 33, 35, 35, 29, 28, 26, 25, 34, 11, 16, 19, 11, 13, 36, 12, 12, 12, 26, 36, 16, 26, 22, 15, 29, 38, 34, and 30. Set the classwidth at 5. Note: a convenient way of doing this is simply to copy and paste these values directly into the R Console (see Comment1 below).
Answer:
#Comment1. Use the c() function and read result into object E2_2.
E2_2 <- c(24, 29, 34, 29, 37, 26, 30, 34, 30, 11, 12, 14, 18, 38, 17, 13, 16, 12, 33, 35, 35, 29, 28, 26, 25, 34, 11, 16, 19, 11, 13, 36, 12, 12, 12, 26, 36, 16, 26, 22, 15, 29, 38, 34, 30)
#Comment2. Read data into the object brks.
brks <- c(10, 14.99, 19.99, 24.99, 29.99, 34.99, 39.99)
#Comment3. Use cut() function to assign values in E2_2 to categories
#defined by brks: (10,15], (15,20], (20,25], (25,30], (30,35],
#(35,40]; read this result into object named categ.
categ <- cut(E2_2, brks)
#Comment4. Use table() function to produce frequency distribution of
#data items in categ; read the result into object fd.
fd <- table(categ)
#Comment5. Examine contents of fd.
fd
## categ
## (10,15] (15,20] (20,25] (25,30] (30,35] (35,40]
## 11 7 2 10 8 7
Thus, 11 values fall in the first category (between 10 and 15), 7 in the second (from 15 to 20), 2 in the third, 10 in the fourth, 8 in the fifth, and 7 in the sixth.
7. Create a relative frequency distribution of the E2_2 data.
Answer:
#Comment1. Create relative frequencies by dividing each element in
#fd by total number of data values; read result into object rf.
rf <- fd / sum(fd)
#Comment2. Examine contents of rf.
rf
## categ
## (10,15] (15,20] (20,25] (25,30] (30,35] (35,40]
## 0.24444444 0.15555556 0.04444444 0.22222222 0.17777778 0.15555556
Thus, 0.24 of observations fall in the first class, 0.16 fall in the second, 0.04 in the third, 0.22 in the fourth, 0.18 in the fifth, and 0.16 fall in the sixth class.
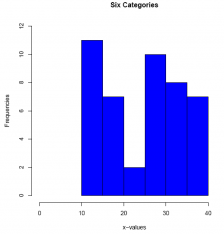
8. Show the histogram of the frequencies for the E2_2 data. Set the range of the horizontal axis between 0 and 45, the range of the vertical axis between 0 and 12. Add a main title and labels for the vertical and horizontal axes. Specify that the classwidth is 5; set blue as the color.
Answer:
#Comment. Use the hist() function to create a histogram
hist(E2_2,
breaks = c(9.99, 14.99, 19.99, 24.99, 29.99, 34.99, 39.99),
xlim = c(0, 45),
ylim = c(0, 12),
xlab = 'x-values',
ylab = 'Frequencies',
main =' Six Categories',
col = 'blue')
9. Create a five-category frequency distribution for the a data set (found on companion website). Read a into the object named E2_3. Hint: first determine a good width for the categories. Note: questions 9 and 10 form two parts of the same question.
Answer:
#Comment1. Import the a data set into the object E2_3.
E2_3 <- a
#Comment2. Use summary() function to find the smallest and largest
#values as well as the mean and median of E2_3.
summary(E2_3)
## var1
## Min. : 6.721
## 1st Qu. :28.336
## Median :51.181
## Mean :50.010
## 3rd Qu. :70.345
## Max. :97.739
Since the smallest value is 6.721 and the largest is 97.74, we need to partition the histogram into ve categories roughly (97.74–6.721/5) = 91.02=5 ≈ 20 units wide. Since the median and mean are almost equal, the data may be normally (or at least symmetically) distributed.
10. Create a frequency distribution for E2_3. Hint: first use the names() function to determine what the variable name might be.
Answer:
#Comment1. Use the names() function to determine the variable name.
names(E2_3)
## [1] "var1"
#Comment2. Read data into the object brks.
brks <- c(0, 20, 40, 60, 80, 100)
#Comment3. Use the cut() function to assign values in E2_3 to
#categories defined by brks: (0,20], (20,40], (40,60], (60,80],
#(80,100]; read this result into object named categ.
categ <- cut(E2_3$var1, brks)
#Comment4. Use table() function to produce frequency distribution of
#data items in categ and read result into object fd.
fd <- table(categ)
#Comment5. Examine contents of fd.
fd
## categ
## (0,20] (20,40] (40,60] (60,80] (80,100]
## 18 68 30 67 16
Thus, there are 18 values falling in the first category, 68 in the second, 30 in the third, 67 in the fourth, and 16 in the fifth. It appears that a frequency distribution with 5 classes spreads out and classifes the 199 data items pretty well. Interestingly, although the summary statistics seem to suggest that the distribution might be somewhat normally distributed—since the mean and median are nearly equal—
the frequency distribution makes clear that the data are not distributed normally, but bimodally.
11. Show the relative frequency distribution of the E2_3 data.
Answer:
#Comment1. Create relative frequencies by dividing fd by total
#number of data values. Read result into object named rf.
rf <- fd / sum(fd)
#Comment2. Request the relative frequency distribution.
rf
## categ
## (0,20] (20,40] (40,60] (60,80] (80,100]
## 0.09045226 0.34170854 0.15075377 0.33668342 0.08040201
Thus, 0.09 (of counts) fall in the first category, 0.34 fall in the second, 0.15 in the third, 0.34 in the fourth, and 0.08 in the fifth.
12. Show the histogram using the 5 categories. Include a main title and labels for the horizontal axis. Define the range of the vertical axis from 0 to 80, and set purple as the color.
Answer:
#Comment. Use the hist() function to create a histogram.
hist(E2_3$var1,
breaks = c(0, 20, 40, 60, 80, 100),
col = 'purple',
ylim = c(0, 80),
xlab = 'x values',
ylab = 'Frequencies',
main = 'Five Categories')
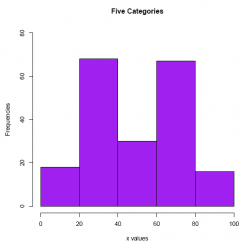
The histogram makes clear that even though the central tendency of the distribution is about 50 (according to the mean and the median), the data are indeed bimodal, not normal.
13. Show the histogram with 10 classes. Does the added precision of 10 classes provide any additional insight when attempting to interpret the distribution of the data set? Once again, add a main title and labels for the vertical and horizontal axes. Specify the range of the vertical axis running from 0 to 40, and set green as the color.
Answer:
#Comment. Use function hist() to create a histogram.
hist(E2_3$var1,
breaks = 10,
col = 'green',
ylim = c(0, 40),
xlab = ' x values',
ylab = 'Frequencies' ,
main = '10 Categories')
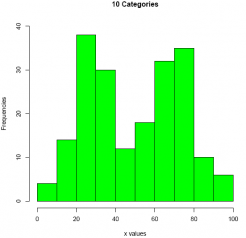
(Note that instead of defining the classes using breaks=c() as we did in the previous exercise, we can also use breaks=10. See the second argument of the hist ()function above.)
On closer inspection, it appears that using 10 categories rather than 5 offers no further resolution to the distribution of the data values. Even so, it is sometimes advantageous to break up the data into more (but narrower) categories because patterns that were not discernable with a smaller number of categories may be revealed when the data are spread out into more categories.
The next three exercises provide a bit of practice writing basic R code for the purpose of creating an image and interpreting its meaning. The three data sets are plot1, plot2, and plot3, and can be found on the companion website.
14. The data set plot1 can be found on the website. Describe the relationship between the two variables. Which descriptive method do you think works best in this case?
Answer:
#Comment1. Use the head(,3) function to identify the variable
#names and first 3 data records.
head(plot1, 3)
## x y
## 1 -3 4
## 2 -3 3
## 3 -2 3
#Comment2. Use the plot() function to create a scatter diagram
#of the two variables.
plot(plot1$x, plot1$y,
pch = 21,
col = "blue",
xlab = "x",
ylab = "y")
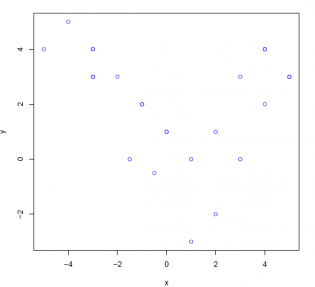
The scatter plot probably works best of all because it provides a picture of the association between two variables very clearly. In this case, the relationship between the two variables x and y is not linear but more parabolic.
15. The data set plot2 can be found on the website. Describe the relationship between the two variables.
Answer:
#Comment1. Use the head(,3) function to identify the variable
#names and first 3 data records.
head(plot2, 3)
## x y
## 1 -23 24
## 2 -33 50
## 3 1 9
#Comment2. Use the plot() function to create a scatter diagram
#of the two variables.
plot(plot2$x, plot2$y,
pch = 23,
col = "red",
xlab = "x",
ylab = "y")
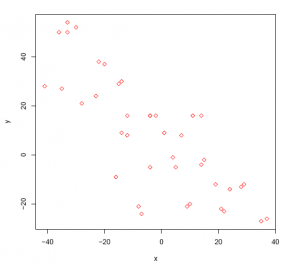
The two variables x and y appear to be negatively (and linearly) related.
16. The data set plot3 can be found on the website. Describe the relationship between the two variables.
Answer:
#Comment1. Use the head(,3) function to identify the variable
#names and first 3 data records.
head(plot3, 3)
## x y
## 1 -3 -4
## 2 15 9
## 3 23 21
#Comment2. Use the plot() function to create a scatter diagram
#of the two variables.
plot(plot3$x, plot3$y,
pch = 25,
col = "purple",
xlab = "x",
ylab = "y")
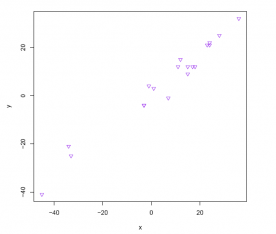
The variables x and y seem to be positively (and linearly) related.
The following exercises use the Cars93 data set that includes information on 93 makes and models of passenger vehicles on sale in the US in 1993. Since Cars93 must be downloaded from the MASS package, be sure to follow the directions provided at the beginning of the Chapter 2 end-of-chapter exercises in the book.
#Comment. Load the MASS package (contains the Cars93 data set).
library(MASS)
##
## Attaching package: 'MASS'
## The following object is masked from 'package:introstats':
##
## housing
17. Report the first 7 observations and first 7 columns (variables) of the Cars93 data set. As a first step, import the data set into the object E2_4. Provide a frequency distribution of the variable Type.
Answer:
#Comment1. Read Cars93 data set into the object E2_4.
E2_4 <- Cars93
#Comment2. Use head() to display the 7 rows and 7 columns of Cars93.
head(E2_4[1 : 7], 7)
## Manufacturer Model Type Min.Price Price Max.Price MPG.city
## 1 Acura Integra Small 12.9 15.9 18.8 25
## 2 Acura Legend Midsize 29.2 33.9 38.7 18
## 3 Audi 90 Compact 25.9 29.1 32.3 20
## 4 Audi 100 Midsize 30.8 37.7 44.6 19
## 5 BMW 535i Midsize 23.7 30.0 36.2 22
## 6 Buick Century Midsize 14.2 15.7 17.3 22
## 7 Buick LeSabre Large 19.9 20.8 21.7 19
#Comment3. Use the table() function to produce a frequency
#distribution of Type; read the result into the object named fd.
fd <- table(E2_4$Type)
#Comment4. Examine the contents of fd.
fd
##
## Compact Large Midsize Small Sporty Van
## 16 11 22 21 14 9
As the frequency distribution of Type indicates, the 93 vehicles are distributed across 6 vehicle types: 22 vehicles are midsize, 21 are small, 16 are compact, 14 are sporty, 11 are large, and 9 are vans.
18. Produce the relative frequency distribution of vehicle Type for the Cars93 data and read the result into object named rfd. What percentage are large cars? Verify that all the proportions (percentages) add up to 1.
Answer:
#Comment1. Divide frequency distribution by number of observations.
#Assign the result to the object named rfd.
rfd <- fd / nrow(E2_4)
#Comment2. To examine the contents of rfd.
rfd
##
## Compact Large Midsize Small Sporty Van
## 0.17204301 0.11827957 0.23655914 0.22580645 0.15053763 0.09677419
#Comment3. Check to make sure the proportions sum to 1.
sum(rfd)
## [1] 1
The proportion of large passenger vehicles in the Cars93 data set is almost 0.12 (0.11828), or roughly 12%. When added up, the proportions sum to one.
19. Produce a bar graph of the relative frequencies of the Type variable in the Cars93 data set. Define the colors of the bars, from left to right, as red, blue, yellow, purple, orange, and green. Set the range of the vertical axis to run between 0 and 0.25. Add "Vehicle Types" as a label for the horizontal axis, "Relative Frequencies" for the vertical axis. Finally, add "Relative Frequencies of Vehicle Types" as a main title.
Answer:
#Comment. Use the barplot() function to provide the bar graph.
barplot(rfd,
col = c('red','blue','yellow','purple','orange','green'),
xlab ='Vehicle Types',
ylab ='Relative Frequencies',
main ='Relative Frequencies of Vehicle Types,
ylim = c(0, 0.25))
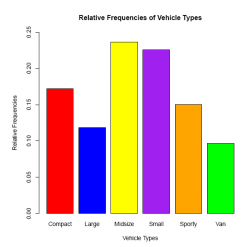
20. Produce the dot plot of the relative frequencies of the Type variable in the Cars93 data set. Remember to use the sort() function to rank order the vehicle types from most representative to least. Set the dot plot points as blue, and include "Relative Frequencies" as a label for the horizontal axis. Finally, add "Relative Frequencies of Vehicle Types" as a main title.
Answer:
#Comment. Use the dotchart() function to create a dot plot
dotchart(sort(rfd),
main ='Relative Frequencies of Vehicle Types',
xlab ='Relative Frequencies',
pch = 20,
col ='blue')
## Warning in dotchart(sort(rfd), main = "Relative Frequencies of Vehicle
Types", : 'x' is neither a vector nor a matrix: using as.numeric(x)
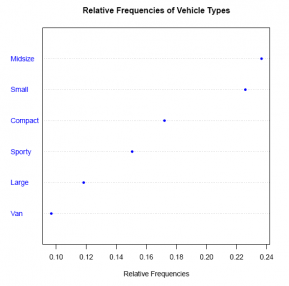
21. Using the data set Cars93, provide a frequency distribution of the variable Max.Price (the maximum price for each of the 93 makes and models). Set the classwidth at 10, defining the lowest price range at or below $10, 000, the second-from-lowest price range from $10, 000 to $20, 000, up to the highest price range of $70, 000 to $80; 000. Comment on the distribution of prices across the 93 vehicles in Cars93.
Answer:
#Comment1. Read data into the object brks.
brks <- c(0, 10, 20, 30, 40, 50, 60, 70, 80)
#Comment2. Use the cut() function to assign values in E2_4 to
#categories defined by brks: (0,10], (10,20], (20,30], (30,40],
#(40,50], (50,60], (60,70],and (70,80]; read this result into
#object named categ.
categ <- cut(E2_4$Max.Price, brks)
#Comment3. Use the table() function to make frequency distribution
#of data items in categ. Read the result into object named fd.
fd <- table(categ)
#Comment4. Examine the contents of fd.
fd
## categ
## (0,10] (10,20] (20,30] (30,40] (40,50] (50,60] (60,70] (70,80]
## 8 39 30 11 3 1 0 1
The frequency distribution indicates that only 5 vehicles have prices above $40, 000; 8 have prices at $10, 000 or below. Most vehicles, 69 of them, are priced in the $10, 000 to $30, 000 range.
22. Find the relative frequencies of the Max.Price variable of the Cars93 data. Comment on the price ranges, and make sure that the relative frequencies sum to one.
Answer:
#Comment1. Create relative frequencies by dividing fd by total
#number of data values. Read the result into object named rfd.
rfd <- fd / sum(fd)
#Comment2. Examine contents of rfd.
rfd
## categ
## (0,10] (10,20] (20,30] (30,40] (40,50] (50,60]
## 0.08602151 0.41935484 0.32258065 0.11827957 0.03225806 0.01075269
## (60,70] (70,80]
## 0.00000000 0.01075269
#Comment3. Check to make sure the relative frequencies sum to 1.
sum(rfd)
## [1] 1
From the relative frequencies, it is clear that nearly 75% of the maximum prices for all passenger vehicles in the Cars93 data set fall in the $10, 000 to $30, 000 range; just over 17% are priced over $30, 000 while less than 9% come in at under $10, 000. All frequencies sum to one.
23. Produce a histogram of the frequencies of the Max.Price variable from the Cars93 data. Set the colors for the histogram bars (running from left to right) as: red, pink, blue, yellow, purple, orange, grey, and green. Add "Maximum Price of Passenger Vehicles (in $000)" as a label for the horizontal axis; include the main title Frequencies of Prices." Include breaks=8 as an argument of the hist() function.
Answer:
#Comment. Use the hist() function with breaks=8.
hist(E2_4$Max.Price,
breaks = 8,
xlab ='Maximum Price of Passenger Vehicles (in $000)',
main ='Frequencies of Prices,
col = c('red','pink','blue,'yellow','purple','orange','grey','green'))
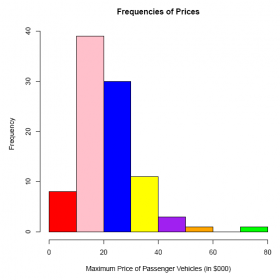
The frequency distribution as depicted by the histogram appears to be slightly skewed (from the normal distribution) to the right. Two outliers appear, one at $80, 000 (the Mercedes Benz 300E) and one at $50, 400 (the In niti Q45).
24. Organize the Cars93 data into a basic cross-tabulation table that reports vehicle Type against the country of Origin. In this particular sample, is it true that most of the large vehicles are of US-origin?
Answer:
#Comment1. Use the table() function to create a cross-tabulation
#table of Type and Origin. Name the resulting object crosstab.
crosstab <- table(E2_4$Type, E2_4$Origin)
#Comment2. Exam the contents of crosstab.
crosstab
##
## USA non-USA
## Compact 7 9
## Large 11 0
## Midsize 10 12
## Small 7 14
## Sporty 8 6
## Van 5 4
As the cross-tabulation table makes clear, all of the large vehicles are of US-origin.
25. Organize the Cars93 data into cross-tabulation with the variables Man.trans.avail (is a manual transmission available?) and Origin organized along the two margins.
#Comment1. Use the table() function to create a cross-tabulation
#table of Man.trans.avail and Origin. Read the result into the
#object named crosstab.
crosstab <- table(E2_4$Man.trans.avail, E2_4$Origin)
#Comment2. Examine the contents of crosstab.
crosstab
##
## USA non-USA
## No 26 6
## Yes 22 39
26. Add column and row totals to the cross-tabulation of Man.trans.avail and Origin of the Cars93 data. Are US vehicles more likely (than non-US vehicles) to offer buyers the option of a manual transmission?
#Comment1. Use the rowSums() function to get totals across rows of
#crosstab; name the result Totals.
Totals <- rowSums(crosstab)
#Comment2. Use the cbind() function to bind column Totals to
#crosstab; recycle the result into the object crosstab.
crosstab <- cbind(crosstab, Totals)
#Comment3. Use the colSums() function to get totals down columns of
#crosstab; name the result Totals.
Totals <- colSums(crosstab)
#Comment4. Use the rbind() function to bind row Totals to crosstab;
#recycle the result into the object crosstab.
crosstab <- rbind(crosstab, Totals)
#Comment5. Examine the contents of crosstab.
crosstab
## USA non-USA Totals
## No 26 6 32
## Yes 22 39 61
## Totals 48 45 93
The cross-tabulation table makes clear that a much larger percentage of vehicles offering buyers the option of a manual transmission are of non-US origin, 87% (or 39 of 45) to only 46% (or 22 of 48) for vehicles of US origin.
27. Organize the Cars93 data into a cross-tabulation with variables Max.Price and EngineSize. Collapse the number of price categories to four|(0,20], (20,40], (40,60], and (60,80]|and the number of engine size categories (in liters of displacement) to three|(0,2], (2,4], and (4,6].
Answer:
#Comment1. Read data into the object brks.
brks <- c(0, 2, 4, 6)
#Comment2. Use the cut() function to assign values in E2_4
#(EngineSize) to categories defined by brks: (0,2], (2,4],
#and (4,6]; read this result into object named displacement.
displacement <- cut(E2_4$EngineSize, brks)
#Comment3. Read data into the object brks.
brks <- c(0, 20, 40, 60, 80)
#Comment4. Use the cut() function to assign values in E2_4
#(Max.Price) to categories defined by brks: (0,20], (20,40],
#(40,60], and (60,80]; read this result into object named price.
price <- cut(E2_4$Max.Price, brks)
#Comment5. Use the table() function to create a cross-tabulation
#table of EngineSize and Max.Price. Name the table crosstab.
crosstab <- table(displacement, price)
#Comment6. Exam the contents of crosstab.
crosstab
## price
## displacement (0,20] (20,40] (40,60] (60,80]
## (0,2] 27 2 0 0
## (2,4] 18 35 1 1
## (4,6] 2 4 3 0
28. For the crosstabulation table of the Cars93 data set (variables are Max.Price and EngineSize), rename the rows: 1 to 2 liters, 2 to 4 liters, and 4 to 6 liters. Rename the columns: Economy, Mid-Price, Higher-Price, and Luxury.
Answer:
#Comment1. Apply rownames() function to crosstab, incorporating
#the new row names: 1 to 2 liters, 2 to 4 liters, 4 to 6 liters.
rownames(crosstab) <- c('1 to 2 liters','2 to 4 liters','4 to 6 liters')
#Comment2. Apply colnames() function to crosstab, incorporating
#the new column names: Economy, Mid-Price, Higher-Price, Luxury.
colnames(crosstab) <- c('Economy','Mid-Price','Higher-Price','Luxury')
#Comment3. Examine contents of crosstab.
crosstab
## price
## displacement Economy Mid-Price Higher-Price Luxury
## 1 to 2 liters 27 2 0 0
## 2 to 4 liters 18 35 1 1
## 4 to 6 liters 2 4 3 0
29. Add row and column totals to the cross-tabulation table of the Cars93 data set where the variables are Max.Price and EngineSize.
Answer:
#Comment1. Use the rowSums() function to get totals across rows of
#crosstab; name the result Totals.
Totals <- rowSums(crosstab)
#Comment2. Use the cbind() function to bind column Totals to crosstab;
#recycle the result into the object crosstab.
crosstab <- cbind(crosstab, Totals)
#Comment3. Use the colSums() function to get totals down columns of
#crosstab; name the result Totals.
Totals <- colSums(crosstab)
#Comment4. Use the rbind() function to bind row Totals to crosstab;
#recycle the result into the object crosstab.
crosstab <- rbind(crosstab, Totals)
crosstab <- rbind(crosstab, Totals)
#Comment5. Examine the contents of crosstab.
crosstab
crosstab
## Economy Mid-Price Higher-Price Luxury Totals
## 1 to 2 liters 27 2 0 0 29
## 2 to 4 liters 18 35 1 1 55
## 4 to 6 liters 2 4 3 0 9
## Totals 47 41 4 1 93
30. Use a scatter plot to reveal the relationship, if any, between EngineSize and Max.Price (in the Cars93 data set). Include A Scatter Diagram Relating Engine Size and Price as a main title. Define the axes as Vehicle Price and Engine Displacement in Liters. Specify the plotting character as orange in color and diamond in shape. Comment on the relationship between the two variables.
Answer:
#Comment. Use the plot() function with Max.Price on the horizontal
#axis, EngineSize on the vertical.
plot(E2_4$Max.Price, E2_4$EngineSize,
main ='A Scatter Diagram Relating Engine Size and Price',
pch = 23,
col ='orange',
ylab ='Engine Displacement in Liters',
xlab ='Vehicle Price')
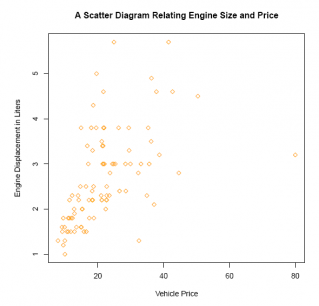
In general, there appears to be a positive relationship between engine size and price: engine size is (roughly) positively related to vehicle price.
31. Construct a scatter plot (using the Cars93 data set) of two variables: EngineSize (in liters of displacement) against Horsepower (maximum horsepower). Add label names Maximum Horsepower and Engine Displacement in Liters to the vertical and horizontal axes, respectively. Also include A Scatter Diagram Relating Engine Size and Horsepower as a main title; set blue as the plotting character color. Comment on the relationship.
Answer:
#Comment. Use the plot() function with EngineSize on the horizontal
#axis, Horsepower on the vertical.
plot(E2_4$EngineSize, E2_4$Horsepower,
main ='A Scatter Diagram Relating Engine Size and Horsepower',
xlab ='Engine Displacement in Liters',
ylab ='Maximum Horsepower',
pch = 19,
col ='blue')
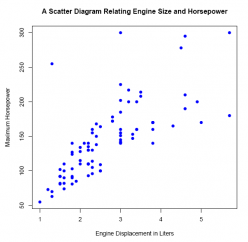
As expected, these two variables are positively and linearly related: in general, the larger the engine, the greater the horsepower.
32. Using the Cars93 data set, create a scatter plot of EngineSize against MPG.highway (highway miles per US gallon by EPA rating). Add label names to the horizontal and vertical axes as well as a main title. Comment on the relationship.
Answer:
#Comment. Use plot() function with EngineSize on the horizontal
#axis, MPG.highway on the vertical.
plot(E2_4$EngineSize, E2_4$MPG.highway,
main ='A Scatter Diagram Relating Engine Size and Miles Per US Gallon',
xlab ='Engine Displacement in Liters',
ylab ='Highway Miles Per US Gallon',
pch = 24,
col ='red')
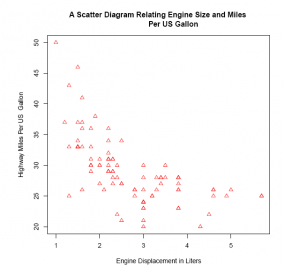
Unsurprisingly, the two variables are negatively (and somewhat linearly) related: in general, the larger the engine size, the lower the gasoline mileage.
33. Making further use of the Cars93 data set, make a scatter plot showing the relationship of two variables: Max.Price and RPM (revolutions per minute). Are these two variables related in a positive or negative manner? Or do they appear to be unrelated? Add the labels Revs per Minute at Maximum Horsepower and Vehicle Price to the vertical and horizontal axes, respectively. Include A Scatter Diagram Relating Vehicle Price and Revs per Minute as a main title. Set purple as the plotting character color.
Answer:
#Comment. Use the plot() function with Max.Price on the horizontal
#axis, RPM on the vertical.
plot(E2_4$Max.Price, E2_4$RPM,
main ='A Scatter Diagram Relating Vehicle Price and Revs per Minute',
ylab ='Revs per Minute at Maximum Horsepower',
xlab ='Vehicle Price',
pch = 20,
col ='purple')
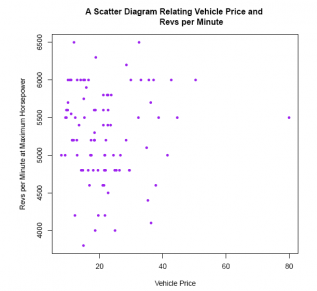
Since there is no reason to suspect that these two particular variables are related, either positively or negatively, we are not surprised to see this cloud of data points.
