Chapter 7: Point Estimation and Sampling Distributions

1. Use the function data[sample(nrow(data),n),] to draw a random sample of n = 9 observations from data set tv_ hours (from the website).

(a) Display the first three rows of data.

Answer:

E7_1 <- tv_hours[sample(nrow(tv_hours), 9), ]

head(E7_1, 3)

##  [1]  10.72   9.94  16.78

(b) Using this sample, what is the point estimate of the population mean µ?

Answer:

mean(E7_1)

##  [1]  12.02667

(c) What is the point estimate of the population standard deviation σ?

Answer:

sd(E7_1)

##  [1]  2.955981

2. During the 2012 US Presidential election, 1500 voters were interviewed upon exiting from a Manhattan polling station where they had just cast their votes. The data are recorded as 1 for a Barack Obama vote and a 0 for a Mitt Romney vote. Draw a random sample of n = 25. Apply function data[sample(nrow(data),n),] and use the data set exit from the website. 

(a) Display all 25 observations.

Answer:

E7_3 <- exit[sample(nrow(exit), 25), ]

E7_3

##  [1] 1 0 0 0 1 1 0 1 0 1 1 1 1 1 1 1 0 1 0 1 1 1 0 1 1

(b) Using this sample, find the point estimate of the population proportion.

Answer:

mean(E7_3)
##  [1]   0.68

3. The mean level of debt carried by students graduating from US universities has now reached $27000 (Forbes, January 29, 2013). Use this value as the population mean and assume that the population standard deviation is = $4500. Suppose an SRS of size n = 121 is selected. Use R to answer the following questions. 

(a) What is the probability that 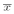fig will fall within ± $500 of µ? That is, what is p(26500 ≤ 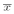fig ≤ 27500)?

Answer: 0.7784.

p(26500 ≤ 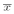fig ≤ 27500) = p(−1.22 ≤ z ≤ +1.22) = 0.7784

pnorm(27500, 27000, 4500 / sqrt(121)) -

pnorm(26500, 27000, 4500 / sqrt(121))

##  [1]   0.7783764

(b) What is the probability that 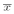fig will fall within ±$250 of µ? That is, what is p(26750 ≤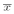fig ≤ 27250)?

Answer: 0.4589.

p(26750 ≤ 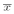fig ≤ 27250) = p(−0.61 ≤ z ≤ +0.61) = 0.4589

pnorm(27250, 27000, 4500 / sqrt(121)) -

pnorm(26750, 27000, 4500 / sqrt(121))

##  [1]  0.458874

4. The percentage of people who are left-handed is not known with certainty but it is thought to be about 12%. Assume the population proportion of left-handed people is p = 0.12. 

(a) If a sample of n = 400 people is chosen randomly, what is the probability that the proportion of left-handers will be within ±0.02 of p? Put another way, what is p(0.10 ≤ 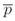fig ≤ 0.14)?

Answer: 0.7816.

p(0.10 ≤ 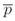fig ≤ 0.14) = p(−1.23 ≤ z ≤ +1.23) = 0.7816

pnorm(0.14, 0.12, sqrt((0.12) * (0.88) / (400))) -

pnorm(0.10, 0.12, sqrt((0.12) * (0.88) / (400)))

##  [1]   0.7816453

(b) If a sample of n = 800 people is chosen randomly, what is the probability that the proportion of left-handers will be within ±0.02 of p? Put another way, what is p(0.10 ≤ 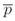fig ≤ 0.14)?

Answer: 0.9183

p(0.10 ≤ 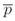fig ≤ 0.14) = p(−1.74 ≤ z ≤ +1.74) = 0.9183

pnorm(0.14, 0.12, sqrt((0.12) * (0.88) / (800))) -

pnorm(0.10, 0.12, sqrt((0.12) * (0.88) / (800)))

##  [1]   0.9182772

5. A quality control inspector is always on the lookout for substandard parts and components provided to her manufacturing company by outside suppliers. Because most shipments contain some defective items, each must be subjected to inspection. Naturally, some shipments contain more defectives than others, and it is the job of the inspector to identify the most defective-laden shipments so that they can be returned to the supplier. Suppose the inspector selects a sample of n = 100 items from a given shipment for testing. Unbeknownst to the inspector, this particular shipment includes 9% defective components. If the policy is to return any shipment with at least 5% defectives, what is the probability that this bad shipment will be accepted as good anyway?

Answer: 0.0811.

p(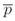fig ≤ 0.05) = p(z ≤ −1.40) = 0.0811

pnorm(0.05, 0.09, sqrt((0.09) * (0.91) / (100)))

##  [1]   0.08109962