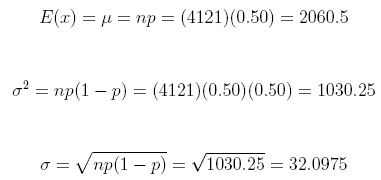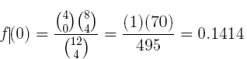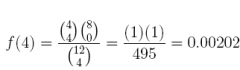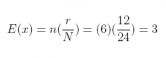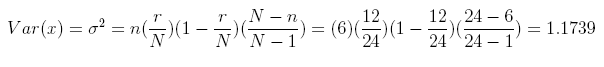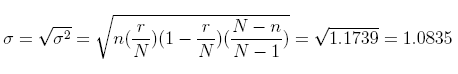1. Suppose we have an experiment which consists of flipping a coin three times.
(a) List the elements of the sample space.
Answer:
S = {(HHH); (HHT); (HTH); (THH); (HTT); (THT); (TTH); (TTT)}
(b) Define the random variable x that describes the number of tails.
Answer: Let x be the number of tails occurring on three coin flips
(c) Since a random variable is a quantitative characterization of the experimental outcome, what is the value of x for each sample point in the sample space?
Answer:

2. Referring to the previous exercise, provide the entire probability distribution of the
random variable x along with the associated probability function f(x).
Answer: when x = 0, f(0) = 0:1250; when x = 1, f(1) = 0:3750; when x = 2, f(2) = 0:3750; and when x = 3, f(3) = 0:1250
3. Again, referring to the previous exercise, is this a valid probability distribution?
Answer: Yes, this is a valid probability distribution since for all values i of f(xi)

and 
4. Referring again to the previous exercise, what is the probability that the random variable x is less than or equal to 2?
Answer:

5. Referring once more to the previous exercise, what is E(x)?
Answer: Answer: E(x) = 1:50

6. For each binomially-distributed random variable x, provide the expected value, the variance, and the standard deviation.
Answer:

Answer:
E(x) =µ = np = (40)(0:70) = 28

Answer:

(d) n = 4121 and p = 0:50
Answer:
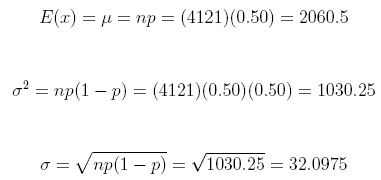
Answer:

Answer:

7. If 85% of vehicles arriving at the Lincoln Tunnel (connecting New Jersey and New York City) have either New York or New Jersey license plates, what is the probability that, of the next 20 vehicles, 2 or fewer (that is, 0, 1, or 2) will bear license plates from states other than New Jersey or New York?

#Comment1. Use the function dbinom(x,n,p) for x=0,1,and 2 and sum.
dbinom(0, 20, 0.15) + dbinom(1, 20, 0.15) + dbinom(2, 20, 0.15)
## [1] 0.4048963
#Comment2. Use function pbinom(x,n,p) to find cumulative binomial
#probabilities. When n=20 and p=0.15, then p(x=0)+p(x=1)+p(x=2) is:
#pbinom(2,20,0.15)=dbinom(0,20,0.15)+dbinom(1,20,0.15)+
#dbinom(2,20,0.15).
pbinom(2, 20, 0.15)
## [1] 0.4048963
#Comment3. Use sum(dbinom()) to confirm.
sum(dbinom(0 : 2, 20, 0.15))
## [1] 0.4048963
8. Find the binomial probability for each exercise below. Label each parameter as x, n, and p, and submit to dbinom(x,n,p). Hint: remember that we can answer each question by simply hitting the up arrow (to recover the dbinom() function) and entering the required n, x, and p values as needed. Any function, not only the dbinom() function, can be recycled repeatedly in this way.
(a) n = 50, x = 10, and p = 0:20
Answer: 0.1398
#Comment. Use function dbinom() and n, x, and p.
n = 50
x = 10
p = 0.20
dbinom(x, n, p)
## [1] 0.139819
(b) n = 40, x = 20, and p = 0:40
Answer: 0.05541
#Comment. Use function dbinom() and n, x, and p.
n = 40
x = 20
p = 0.40
dbinom(x, n, p)
## [1] 0.05541415
(c) n = 30, x = 10, and p = 0:30
Answer: 0.1416
#Comment. Use function dbinom() and n, x, and p.
n = 30
x = 10
p = 0.30
dbinom(x, n, p)
## [1] 0.1415617
(d) n = 50, x = 30, and p = 0:70
Answer: 0.03704
#Comment. Use function dbinom() and n, x, and p.
n = 50
x = 30
p = 0.70
dbinom(x, n, p)
## [1] 0.03703876
(e) n = 40, x = 20, and p = 0:60
Answer: 0.05541
#Comment. Use function dbinom() and n, x, and p.
n = 40
x = 20
p = 0.60
dbinom (x, n, p)
## [1] 0.05541415
(f) n = 30, x = 10, and p = 0:40
Answer: 0.1152
#Comment. Use function dbinom() and n, x, and p.
n = 30
x = 10
p = 0.40
dbinom(x, n, p)
## [1] 0.1151854
9. At a large public university, half the students enrolled in a statistics class take the course on a pass-fail basis; the other half take it for a normal grade of A,...,F.
(a) If 20 students are selected at random, what is the probability that 12 (of the 20) are taking the course pass-fail?
Answer: 0.1201
#Comment. Use the function dbinom(x,n,p).
dbinom(12, 20, 0.50)
## [1] 0.1201344
(b) What is the probability that no more than 5 students are taking the course for a normal grade of A,...,F?
Answer: 0.02069
#Comment1. Use pbinom(x,n,p) for cumulative probabilities.
pbinom(5, 20, 0.50)
## [1] 0.02069473
#Comment2. Use sum(dbinom()) to confirm.
sum(dbinom(0 : 5, 20, 0.50))
## [1] 0.02069473
(c) What is the expected number who are taking the course on a pass-fail basis?
Answer: E(x) = np = (20)(0:50) = 10 students.
10. Suppose x is a Poisson-distributed random variable with an expected value of 3 occurrences per interval. Please answer the following questions.
(a) What is the Poisson probability function f(x)?
Answer:

(b) For this probability distribution, what is p(x = 2)?
Answer: 0.224

#Comment. Use the function dpois(x,mu) for Poisson probability.
dpois(2, 3)
## [1] 0.2240418
(c) For this probability distribution, what is p(x = 3)?
Answer: 0.224

#Comment. Use the function dpois(x,mu) for Poisson probability.
dpois(3, 3)
## [1] 0.2240418
(d) What are the Poisson probabilities of x = 0, 1,..., 4 for µ = 3?
Answer:
#Comment. Use function dpois(0:4,mu) for the 5 probabilities.
dpois(0 : 4, 3)
## [1] 0.04978707 0.14936121 0.22404181 0.22404181 0.16803136
(e) What are the Poisson probabilities of x = 5, 6, 7, 8 for µ = 3?
Answer:
#Comment. Use function dpois(5:8,mu) for the 4 probabilities.
dpois(5 : 8 , 3)
## [1] 0.100818813 0.050409407 0.021604031 0.008101512
11. A Poisson process has an expected value of 5 occurrences per interval.
(a) What is the Poisson probability function f(x)?
Answer:

(b) What is the expected number of occurrences in 5 intervals?
Answer: The expected number of occurrences is 25 for 5 intervals.
(c) What is the new probability function for 5 intervals?
Answer:

(d) What is the expected number of occurrences in 0.25 intervals?
Answer: The expected number of occurrences is 1.25 for 0.25 intervals.
(e) What is the new probability function for 0.25 intervals?
Answer:

12. If µ = 1.25, what is the probability of x = 0, 1, 2, 3 occurrences? Use f(x) and R.
Answer: f(0) = 0:2865; f(1) = 0:35813; f(2) = 0:22383; and f(3) = 0:09326

#Comment. Use function dpois(0:3,mu) for the 4 probabilities.
dpois(0 : 3, 1.25)
## [1] 0.28650480 0.35813100 0.22383187 0.09326328
13. If µ = 25, what is probability of x = 23, 24, 25, 26 occurrences? Use f(x) and R.
Answer: f(23) = 0:07634; f(24) = 0:07952; f(25) = 0:07952; and f(26) = 0:07646

#Comment. Use function dpois(23:26,mu) for the 4 probabilities.
dpois(23 : 26, 25)
## [1] 0.07634203 0.07952295 0.07952295 0.07646438
14. Calls arrive at a customer-service number at the rate of 20 per hour. Use R to answer the following questions.
(a) What is the probability of 5 or more calls in a 15 fteen minute period?
Answer: 0.5595
#Comment1. Convert 20 calls/60 minutes to 5 calls/15 minutes;
#use 1 minus the probability of 4 or fewer calls.
1 - ppois(4, 5)
## [1] 0.5595067
#Comment2. Or subtract from 1 the probabilities of
#x =0,1,2,3 and 4 calls.
1 - (dpois(0, 5) + dpois(1, 5) + dpois(2, 5) + dpois(3, 5) +
dpois(4, 5))
## [1] 0.5595067
(b) What is the probability that between 7 and 12 calls, inclusive, will arrive in the next 30 minutes?
Answer: 0.6614
#Comment1. Convert 20 calls/60 minutes to 10 calls/30 minutes;
#subtract ppois(6,10) from ppois(12,10).
ppois(12, 10) - ppois(6, 10)
## [1] 0.6614151
#Comment2. Or sum probabilities of x=7,8,9,10,11,12.
sum(dpois(7 : 12, 10))
## [1] 0.6614151
(c) If one particular caller has a dicult problem to resolve and requires 15 minutes of the customer-service representative's time, how many callers would we expect to be waiting on hold once the call has been completed?
Answer: Since 20 calls every 60 minutes is equivalent to 5 calls every 15 minutes, we would expect 5 callers to be waiting their turn.
(d) If the customer-service representative wishes to take a 5 minute coffee break, what is the probability that no calls will be waiting once he returns?
Answer: 0.1882
#Comment. Convert 20 calls/60 minutes into
#1.67 calls/5 minutes; use dpois(0,1.67).
dpois(0, 1.67)
## [1] 0.1882471
15. Small aircraft land at a private airport at an average rate of 1 arrival/10 minutes.
Answer: 0.1339

(b) What is the probability that there will be more than 4 arrivals in the next hour?
Answer: 0.7149
#Comment. Use 1 minus probability of 4 or fewer arrivals.
1 - ppois(4, 6)
## [1] 0.7149435
(c) If the airport is open 12 hours a day, what is the probability that fewer than 75 aircraft will arrive in the next day of business (i.e., over the next 12 hours)?
Answer: 0.6227

16. The number of defects associated with a plate glass manufacturing process is Poisson- distributed with a rate of 0.002 defects per square foot. Suppose the manufacturer has received an order for a large plate glass window of dimensions 10 feet by 10 feet.
(a) What is the probability the window will have no defects? 1 defect? 2 defect?
Answer:

(b) What is the probability there will be no more than 2 defects?
Answer: 0.9989
#Comment1. Nest function dpois(0:2,0.20) within function sum().
sum(dpois(0 : 2, 0.20))
## [1] 0.9988515
#Comment2. Or use ppois(2,0.20) to find cumulative probability.
ppois(2, 0.20)
## [1] 0.9988515
(c) What is the probability there will be more than 2 defects?
Answer: 0.001148
#Comment. Use 1 minus probability of 2 or fewer defects.
1 - ppois(2, 0.20)
## [1] 0.001148481
17. As soon as the spring season arrives, many businesses contract for construction jobs they have been delaying over the previous cold winter months. One of the major league baseball teams has decided to resurface with asphalt a large parking area adjacent to their stadium. The dimensions of the surface are 300 feet by 200 feet, or 60,000 square feet. Unfortunately, since asphalt is usually imperfectly applied, there is an average of 0.06 air bubbles per square foot.
(a) What is the probability there will be between 3,500 and 3,700 bubbles, inclusive, in the entire surface?

Answer: 0.9061
#Comment. From ppois(3700,3600) subtract ppois(3499,3600).
ppois(3700, 3600) - ppois(3499, 3600)
## [1] 0.9060769
(b) What is the probability there will be between 3,550 and 3,650 bubbles, inclusive, in the entire surface?
Answer: 0.6000
#Comment. From ppois(3650,3600) subtract ppois(3549,3600).
ppois(3650, 3600) - ppois(3549, 3600)
## [1] 0.6000281
(c) What is the probability there will be more than 3650 bubbles?
Answer: 0.1998
#Comment. Use 1 minus probability of 3650 or fewer bubbles.
1 - ppois(3650, 3600)
## [1] 0.1997592
18. Suppose the number of radioactive particles identified by a sensitive counting device is Poisson-distributed. The particles pass through a certain threshold at a rate of 60 per millisecond. (A millisecond is one-thousandth of a second, or 1/1000 second.)
(a) What is the expected number of occurrences—the count of radioactive particles—in a second?
Answer: 
(b) What is the expected number of occurrences—the count of radioactive particles—in a minute?
(c) What is the expected number of occurrences—the count of radioactive particles—in one-third a millisecond?
(d) What is the probability of between 18 and 21 particles, inclusive, in one-third of a millisecond?
Answer: 0.3467
#Comment1. From ppois(21,20) subtract ppois(17,20).
ppois(21, 20) - ppois(17, 20)
## [1] 0.3466693
#Comment2. Nest function dpois(18:21,20) within function sum().
sum(dpois(18 : 21, 20))
## [1] 0.3466693
19. If N = 12 and r = 4, what are the hypergeometric probabilities f(x) for the following values of x and n?
Note: if N = 12 and r = 4, then (N– r) = (12 – 4) = 8
Recall: the hypergeometric probability function is

which in this case is

Answer: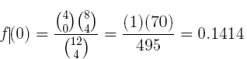
Answer: 
Answer: 
Answer: 
Answer:
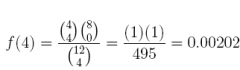
20. Use function dhyper(x,r,N-r,n) to answer all parts of the previous exercise. Hint: copy-and-paste this function along with values for N, r, and n. Then change the value of x for each question; all other values remain the same for all parts.
Answer:
#Comment. Use function dhyper(x,r,N-r,n) for hypergeometric
#probabilities.
N = 12
r = 4
n = 4
x = 0
dhyper(x, r, N - r, n)
## [1] 0.1414141
N = 12
r = 4
n = 4
x = 1
dhyper(x, r, N - r, n)
## [1] 0.4525253
N = 12
r = 4
n = 4
x = 2
dhyper(x, r, N - r, n)
## [1] 0.3393939
N = 12
r = 4
n = 4
x = 3
dhyper(x, r, N - r, n)
## [1] 0.06464646
N = 12
r = 4
n = 4
x = 4
dhyper(x, r, N - r, n)
## [1] 0.002020202
21. Referring to the previous exercise, is there a simplier way to produce these 5 probabilities using R? Do they sum to 1?
Answer:
#Comment1. Use function dhyper(0:4,4,8,4) to find probabilities.
dhyper(0 : 4, 4, 8, 4)
## [1] 0.141414141 0.452525253 0.339393939 0.064646465 0.002020202
#Comment2. Next function dhyper(0:4,4,8,4) within function sum().
sum(dhyper(0 : 4, 4, 8, 4))
## [1] 1
22. If N = 24, r = 12, and n = 6, what are the hypergeometric probabilities f(x) for the following values of x? Note: if N = 24 and r = 12, then (N–r) = (24–12) = 12:
Answer: 0.6798
Summing the probabilities for x = 0, 1, 2, and 3, and using


Answer: 0.3202
Summing the probabilities for x = 4, 5, and 6 using

Answer: 0.8450

23. Use R to confirm the answers to the previous exercise.
Answer:
#Comment1. Use function phyper(x,r,N-r,n) for cumulative probability
N = 24
r = 12
n = 6
x = 3
phyper(x, r, N - r, n)
## [1] 0.6797973
#Comment2. Use 1 minus phyper(x,r,N-r,n) for probability.
N = 24
r = 12
n = 6
x = 3
1 - phyper(x, r, N - r, n)
## [1] 0.3202027
#Comment3. From phyper(4,12,12,6) subtract phyper(1,12,12,6).
N = 24
r = 12
n = 6
phyper(4, r, N - r, n) - phyper(1, r, N - r, n)
## [1] 0.8450474
25. A small manufacturer is concerned with the quality of AA batteries being delivered by a certain supplier. Recently, the average battery life has fallen below the manufacturer's standard, and so the manufacturer has begun to test the life of the batteries from this particular supplier on a regular basis. To do this, the quality control inspector randomly selects small samples of batteries from each shipping carton of 100. If even 1 of the batteries fails the test, the entire box of 100 is rejected and returned to the supplier. Suppose the current carton of 100 batteries contains 15 defective batteries.
(a) What is the probability the carton of 100 batteries will be returned if the sample size is n = 5?
Answer: 0.5643
One way to approach this question is to re-express it as 1 minus the probability the shipment will not be returned, or 1 minus the probability that no defective batteries are detected. Using

for

to find the probability that no defectives are found, we need only subtract this probability from 1.
That is, the probability the shipment will be returned is one minus the probability that no defective batteries are detected.
= 1 – 0:4357 = 0:5643
#Comment. Use 1 minus probability of dhyper(0,15,85,5)
1 - dhyper(0, 15, 85, 5)
## [1] 0.5643167
(b) What is the probability the carton of 100 batteries will be returned if the sample size is n = 10?
Answer: 0.8192
The probability the shipment will not be returned is the probability no defective batteries are detected.

The probability the shipment will be returned is one minus the probability that no defective batteries are detected.
= 1 – 0:1808 = 0:8192
#Comment. Use 1 minus probability of dhyper(0,15,85,10)
1 - dhyper(0, 15, 85, 10)
## [1] 0.8192313
(c) If the quality control department has decided that it wants roughly a 0.85 probability of correctly identifying at least 1 of the 15 defective batteries out of the 100 in the shipping carton, what sample size should they use?
Answer: A sample size of n = 11 results in nearly 0.85 probability that at least one defective item is identified.
Subtract from 1 the probability that no defective items are identified in a sample of size n = 11.

1– 0:1506 = 0:8494
#Comment. Use 1 minus probability of dhyper(0,15,85,11)
1 - dhyper(0, 15, 85, 11)
## [1] 0.8493594
26. Suppose we select a random sample of 5 balls from an urn containing 4 red, 3 white, and 2 blue balls. What is the probability that we draw 2 blue and at least 1 red ball? Please use R.
Answer: 0.2698
Sum the probabilities of the di erent ways one could get 2 blue and at least 1 red ball from the urn.

#Comment. Sum the probabilities of 2 blues and 1, 2, and 3 reds.
(choose(3, 2) * choose(4, 1) * choose(2, 2) +
choose(3, 1) * choose(4, 2) * choose(2, 2) +
choose(3, 0) * choose(4, 3) * choose(2, 2)) / (choose(9, 5))
## [1] 0.2698413