Statistics with R
Student Resources
Chapter 10: Hypothesis Tests About u and p: Applications
1. The Chair of the East Asian languages department at a local university is now mandating that first-year students enroll in conversation-only language laboratories in addition to the typical lecture-based classes that emphasize grammar and vocabulary drills. The purpose of the conversation laboratory sessions is to improve students' comprehension and speaking skills. They are conducted on a weekly basis, one hour per session. After the first semester, the Chair wants to conduct a test to determine if students who participate in the conversation classes perform better than students who have not. The average nal examination result for students from earlier academic years, when no conversation-only laboratories were available, has been 72 (out of a possible of 150). How should the null and alternative hypotheses
be expressed?
Answer:
H0 : µ ≤ 72
H0 : µ > 72
2. Answer the following questions about the previous hypothesis test.
(a) What inference can be drawn if H0 is rejected?
Answer: If H0 is rejected, then it can be inferrred that the conversation language laboratories may indeed help students improve their final examination result. The empirical evidence supports this conclusion.
(b) What if H0 is not rejected?
Answer: If H0 is not rejected, then we would say that the evidence is not strong enough to conclude that the conversation-language laboratories help students improve their final examination result.
3. In view of the above hypothesis test, answer the following questions.
(a) If a Type I error is committed, what mistake is being made?
Answer: We conclude that the conversation-language laboratory helps students improve their final examination results when it does not.
(b) If a Type II error is committed, what mistake is being made?
Answer: We conclude that the conversation-language laboratory does not help students improve their final examination results even though it does.
4. The U.S. Department of Homeland Security has faced mounting criticism over the length of time departing passengers are now forced to wait while clearing security (e.g., searches, metal detectors, passport control) as they prepare to board commerical flights. In view of this, the Homeland Security Department manager at Newark International Airport has taken several measures that he hopes speed up the process of getting air passengers through the Airport and onto their plane. Compounding
the challenge is the fact that the number of passengers passing through Newark has been steadily increasing every month for several years. The Department manager wants to know if the average passenger security clearance waiting time has changed from 39 minutes it was the last time it was measured. If the measures have been successful, the waiting time should be shorter; if the passenger volume at Newark has overwhelmed any measures that might be taken, the waiting time may be longer. How should the Department manager express the null and alternative hypotheses?
Answer:
H0 : µ = 39
H0 : µ ≠ 39
5. Answer the following questions about the previous hypothesis test.
(a) What inference can be drawn if H0 is rejected?
Answer: If H0 is rejected, then it can be inferred that the average waiting time has changed since the last time it was measured, and is either longer or shorter than 39 minutes.
(b) What if H0 is not rejected?
Answer: If H0 is not rejected, then we would say that the evidence is not strong enough to conclude that the average waiting time has changed from 39 minutes.
6. Referring to the previous exercise, answer the following questions.
(a) For this testing situation, what is a Type I error?
Answer: We conclude that the average waiting time has changed when it has not.
(b) What is a Type II error?
Answer: We conclude that the average waiting time has not changed even though it has.
7. In recent years, applications to the Ph.D. programs of 10 selected schools of engineering in the U.S. included 18,522 from foreign students. However, in early 2017, a group of administrators representing American research universities expressed concern that the number of applications to their Ph.D. programs from non-U.S. students might decline. In January 2017, President Donald Trump announced a new policy designed to restrict and otherwise discourage applications from overseas students wishing to pursue Ph.D. degrees in engineering and science. If we wish to test whether his policies are having the intended effect of discouraging and reducing overseas applicants, how should the null and alternative hypotheses be expressed?
Answer:
H0 : µ ≥ 18522
Ha : µ<18522
8. Answer the following questions about the previous hypothesis test.
(a) What inference can be drawn if H0 is rejected?
Answer: If H0 is rejected, then it can be inferred that the number of overseas applicants to Ph.D. programs has fallen.
(b) What if H0 is not rejected?
Answer: If H0 is not rejected, then we would say that the evidence is not strong enough to conclude that the number of overseas applicants to Ph.D. programs has fallen.
9. In reference to the previous exercise, answer the following questions.
(a) Describe a Type I error.
Answer: We conclude that the number of overseas applicants to Ph.D. programs has fallen when it has not.
(b) What is a Type II error.
Answer: We conclude that the number of overseas applicants to Ph.D. programs has not fallen even though it has.
10. The public school board responsible for a district in the U.S. state of Louisiana has decided to take on the obesity problem among high school students by introducing a healthier diet (lower fat, sugar, and salt; more vegetables, less fried food) into the school lunch program. Last year, 19% of adolescent youths, aged 15 to 18 years, were designated obese. In an effort to monitor the success of the new school lunch program, school offcials have decided to collect data from all schools in the district at the end of the first year of implementation. If we let p be the percentage of students classified as obese, how should school officials frame the null and alternative hypotheses ?
Answer:
H0 : p ≥ 0.19
Ha : p<0.19
11. Answer the following questions about the previous hypothesis test.
(a) What inference can be drawn if H0 is rejected?
Answer: If H0 is rejected, then it can be inferred that the obesity rate of high school students has fallen below 19%.
(b) What if H0 is not rejected?
Answer: If H0 is not rejected, then we would say that the evidence is not strong enough to conclude that the obesity rate of high school students has fallen below 19%.
12. In reference to the preceding exercise, answer the following questions.
(a) What is a Type I error?
Answer: We conclude that the obesity rate of high school students has fallen below 19% when it has not.
(b) What is a Type II error?
Answer: We conclude that the obesity rate of high school students has not fallen below 19% even though it has.
13. The percent of purchases made online (rather than at brick-and-mortar retail locations) is increasing each year as more consumers find the internet shopping experience more convenient and economical than that at malls or big-box retail locations. Naturally, this trend poses challenges to traditional brick-and-mortar retailers of all kinds in all developed economies. A Canadian business school professor stated recently that she believed that at least 50% of consumer purchases are now made online. If we were to collect data on the shopping habits from a sample of Canadian households to determine if most consumer purchases (i.e., more than 50%) are now made online, how should we express the null and alternative hypotheses? Let p be the percent of purchases that are made online.
Answer:
H0 : p ≤ 0.50
Ha : p>0.50
14. Answer the following questions about the previous hypothesis test.
(a) What inference can be drawn if H0 is rejected?
Answer: If H0 is rejected, then it can be inferred that online purchases now
make up more than 50% of all Canadian consumer purchases.
(b) What if H0 is not rejected?
Answer: If H0 is not rejected, then we would say that the evidence is not strong enough to conclude that online purchases now make up more than 50% of all Canadian consumer purchases .
15. Referring to the previous exercise, answer the following questions.
(a) What does a Type I error mean?
Answer: We conclude that most Canadian consumer purchases are made online even though they are not .
(b) What is a Type II error?
Answer: We conclude that most Canadian consumer purchases are not made online even though they are.
16. On April 23, 2017, French citizens cast their ballots for the candidates who would face one another in the French Presidential election to be held two weeks later. From the field of four, the two candidates who emerged successful are Emmanuel Macron and Marine Le Pen. Political scientists would like to predict which of the two candidates will ultimately succeed to the Presidency, and so they turn to political polling and statistical analysis to guage the early sentiment among the French voting public. Since both candidates are considered unconventional|neither has run for the Presidency in the past and neither represents one of France's traditional political parties|the early guess is that each candidate has a 50% chance of winning. How should the null and alternative hypotheses tests be structured? Let p be the proportion of voters favoring Marine Le Pen.
Answer:
H0 : p = 0.50
H0 : p ≠ 0.50
17. Answer the following questions about the previous hypothesis test.
(a) What inference can be drawn if H0 is rejected?
Answer: If H0 is rejected, then it can be inferred that the percentage of French voters favoring Marine Le Pen differs from 50%; it is either higher or lower than 50%.
(b) What if H0 is not rejected?
Answer: If H0 is not rejected, then we would say that the evidence is not strong enough to conclude that the percentage favoring Marine Le Pen either exceeds or falls short of 50%.
18. In view of the previous exercise, answer the following questions.
(a) Describe a Type I error.
Answer: We conclude that the percentage of French voters favoring Marine Le Pen differs from 50% when it does not differ.
(b) What is a Type II error.
Answer: We conclude that the percentage of French voters favoring Marine Le Pen does not differ from 50% even though it does.
19.A criminal trial can be seen in terms of a hypothesis test where
H0: defendant is innocent
Ha: defendant is guilty
(a) What is a Type I error?
Answer: A Type I error occurs when we reject H0 when it is true. Therefore, a Type I error in this instance occurs when we convict an innocent person.
(b) What is a Type II error?
Answer: A Type II error happens when we do not reject H0 even though it is false. In this case, a Type II error occurs when we acquit a guilty person.
(c) Although in a criminal trial we do not establish values for α and β, we would ideally like to set the value of lower than for β. Why?
Answer: In the criminal justice system in many countries, including in the U.S., the error of convicting an innocent person is generally considered more serious than the error of acquiting a guilty person. Since α is the probability of a Type I error, we would want to set that value lower than for the probability of a Type II error, β .
20. Referring to the Agrico example (Section 10.1), suppose the quality-control manager decides that while Agrico does not want to under ll its packages, neither does it wish to overfill. Clearly, giving away product in overfilled packages costs Agrico money, and provides little or no goodwill among customers who are unaware they are reaping a windfall in free bran flakes. Suppose that the sample size is adjusted upward to n = 100 and α is reset to 0.10. Using the six-step hypothesis-testing framework, test H0 : µ ≤375 against Ha : µ>375. Recall that σ = 22.5. Suppose the sample of n = 100 provides a mean weight of 377.50 grams. What is the p-value?
Answer:
(a) H0 : µ ≤ 375
(b) Ha : µ>375
(c) n = 100 and α = 0.10
(d) Reject H0 : µ ≤ 375 if z>zα = z0.10 = 1.282. That is
RR : z>1.282 where
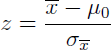
qnorm(0.90)
## [1] 1.281552
(e) Since x̄ = 377.50,
Answer:
![]()
(f) Since z = 1.111<1.282 (and thus does not fall in the RR), we do not reject H0. We cannot conclude from the evidence that Agrico is over lling its packages.
Answer: The p-value = p(z>1.111) = 0.1333.
pnorm(1.111, lower.tail = FALSE)
## [1] 0.1332842
Since p-value = 0.1333> = 0.10, we do not reject H0.
21. Family physicians in Tampa, Florida reportedly earn an average annual salary of $141. 300. Suppose we conduct a survey on a sample of n = 64 family physicians from New Orleans, Louisiana to test whether their mean annual salary is different from the reported mean of $141, 300 in Tampa, and find that the sample mean is $138, 000. Assume σ = $18, 000. At the level of α = 0.01, use the six-step framework
to test H0 : µ = 141, 300; against Ha : µ0 ≠ 141, 300. What is the p-value?
Answer:
(a) H0 : µ = 141, 300
(b) Ha : µ0 ≠ 141, 300
(c) n = 64 and α = 0:01
(d) Reject H0 if z>za/2 = z0.005 = 2.576 or z< – z a/2 = –z0:005 = –2.576. That is
RR : z>2.576 or z< – 2.576 where
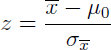
qnorm(0.005)
## [1] -2.575829
qnorm(0.995)
## [1] 2.575829
(e) Since x̄ = 138, 000,
Answer:
![]()
(f) Since z = 1.47<2.576 (and thus does not fall in the RR), we do not reject H0. We cannot conclude from the evidence that New Orleans physician salary is different from Tampa physician salary.
Answer: The p-value = (2)(p(z>1.47)) = 0.1416.
2 * pnorm(1.47, lower.tail = FALSE)
## [1] 0.1415618
Since p-value = 0.1416> α= 0:01, we do not reject H0.
22. Because two Australian students are planning to attend the University of London next academic year, they are searching for a at in the WC1 district of the city, a neighborhood that offers many amenities to the University's students. Even though they plan to share the apartment, they are unwilling to pay more than $4000 per month for rent. As a preliminary step, they want to make sure that the neighborhood they have selected is a realistic choice, given this budgetary constraint, before committing to this particular area. Suppose they search online for rental properties and compile a list of 70 flats in the Russell Square vicinity, along with each property's monthly rent. Use the housing data (from the companion website) to test H0 : µ ≥ 4000 against Ha : µ < 4000 at α = 0.10. The variable name is rent.
Answer:
t.test(housing$rent, mu = 4000, alternative = 'l')
##
## One Sample t-test
#### data: housing$rent
## t = -1.5838, df = 69, p-value = 0.05891
## alternative hypothesis: true mean is less than 4000
## 95 percent confidence interval:
## -Inf 4004.501
## sample estimates:
## mean of x
## 3914.571
Because p-value=0.05891< α = 0.10, we reject H0 : µ ≥ 4000 and conclude that the mean monthly rent is less than $4000.
23. The research director at a major advertising agency believes that people are watching more (rather than less) television during the 2-day holiday period from New Year's Eve through New Year's Day. Before the 2008 financial crisis, when many people traveled during the holidays, the average amount of television viewing during the New Year period was 10 hours. The research director would like to know if
the amount of television viewing has increased as more people decide to stay home over the holidays rather than travel. Assume that television viewing data have been collected across 100 households during the most recent New Year's holiday period. Use the tv hours data (from the companion website), and test H0 : µ ≤ 10 against Ha : µ >10 at the α = 0.01. The variable name is hours.
Answer: options(scipen = 999)
t.test(tv_hours$hours, mu = 10, alternative = 'g' )
##
## One Sample t-test
##
## data: tv_hours$hours
## t = 4.1241, df = 99, p-value = 0.00003877
## alternative hypothesis: true mean is greater than 10
## 95 percent confidence interval:
## 10.97954 Inf
## sample estimates:
## mean of x
## 11.6397
Because p-value=0.00003877< α = 0.01, we reject H0 : µ ≤ 10 and conclude that
the average amount of television viewing over the New Year's holiday period is now
more than 10 hours.
24. The student newspaper at a large business school claims that 55% of graduating students have an offer of employment even before they graduate. The Offce of Student Affairs decided to investigate this claim to see whether it is true. When they carried out the survey, they found that 321 of 535 graduating students reported that they have a job o er. At a level of α = 0.10, use the six-step framework to test
H0 : p = 0.55 against Ha : p ≠ 0.55. What is the p-value?
Answer:
(a) H0 : p = 0.55
(b) Ha : p ≠ 0.55
(c) n = 535 and = 0.10
(d) Reject H0 if z>z a/2 = z0:05 = 1.645 or z<–z a/2 = –z0.05 = –1.645. That is
RR : z>1.645 or z< –1.645 where
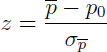
qnorm(0.05)
## [1] -1.644854
qnorm(0.95)
## [1] 1.644854
(e) Since p = 321/535 = 0.60,
Answer:
![]()
(f) Since z = 2.32>1.645, we reject H0 and conclude that the percent of students having jobs upon graduation differs from (and exceeds) 0.55.
Answer: The p-value = (2)(p(z>2.32)) = 0.02034.
2 * pnorm(2.32, lower.tail = FALSE)
## [1] 0.02034088
Since p-value = 0.02034< = 0.10, we reject H0.
Alternatively, we may use the prop.test() function, making sure that we specify the 4 arguments as follows. Note that the positive square root of X-squared = 5.4 (see the fourth line below) is 2.32, which equals the z test statistic above.
prop.test(321, 535, p = 0.55, correct = FALSE)
##
## 1-sample proportions test without continuity correction
##
## data: 321 out of 535, null probability 0.55
## X-squared = 5.404, df = 1, p-value = 0.02009
## alternative hypothesis: true p is not equal to 0.55
## 95 percent confidence interval:
## 0.5579169 0.6406573
## sample estimates:
## p
## 0.6
Note that the p-value=0.02009 is reported on the fourth line from the top.
25. While campaigning for higher political office during a recent election, a certain candidate claimed that \at least 75% of voters want the country to end all foreign aid to all countries." When a polling organization conducted a survey to investigate this claim, they found that 242 out of a sample of n = 346 expressed agreement with the statement. At a level of α = 0.02, use the six-step framework to test
H0 : p ≥ 0.75 against Ha : p<0.75. What is the p-value?
Answer:
(a) H0 : p ≥ 0.75
(b) Ha : p<0.75
(c) n = 346 and a = 0.02
(d) Reject H0 if z< –z = –z0.02 = –2.054. That is
RR : z< – 2.054 where
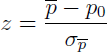
qnorm(0.02)
## [1] -2.053749
![]()
Answer:
![]()
(f) Since z = -2.1727< - 2.054, we reject H0 and conclude that the percent of people favoring elimination of foreign aid is less than 0.75.
Answer:
The p-value = p(z< – 2.1727) = 0.0149.
pnorm(-2.1727)
## [1] 0.01490145
Since p-value = 0:0149< α = 0.02, we reject H0.
Alternatively, we may use the prop.test() function. Note that there are now 5
arguments because this involves a one-tail test.
prop.test(242, 346, p = 0.75, alternative = 'l' , correct = FALSE)
##
## 1-sample proportions test without continuity correction
##
## data: 242 out of 346, null probability 0.75
## X-squared = 4.7206, df = 1, p-value = 0.0149
## alternative hypothesis: true p is less than 0.75
## 95 percent confidence interval:
## 0.0000000 0.7382917
## sample estimates:
## p
## 0.699422
The p-value=0.0149 is reported on the fourth line from the top.
26. An Italian farmer who grows and packs agricultural produce for the export market claims that one of his packages contains 750 grams of tomatoes. To ensure that the company consistently meets this standard, the manager conducts a study to test H0 : µ ≥750 against Ha : µ<750. Based on previous studies, σ = 25. What sample size should the manager use if he wants a 0.90 probability of identifying when the mean weight falls short of 750 grams by 10 grams? Let α = 0.01.
Answer:
if n = 82, then α = 0.01 and β = 0.10.
![]()
((qnorm(0.01, lower.tail = FALSE)) +
(qnorm(0.10, lower.tail = FALSE))) ^ 2 * (25) ^ 2 /
(750 - 740) ^ 2
## [1] 81.35586
