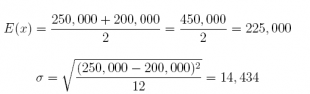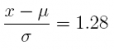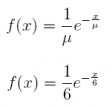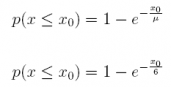Chapter 6: Continuous Probability Distributions
1. A recent college graduate is moving to Houston, Texas to take a new job, and is looking to purchase a home. Since Houston comprises a relatively large metropolitan area of about 7 million people, there are a lot of homes from which to choose. When searching for properties on the real estate websites, it is possible to select the price range of housing in which one is most interested. Suppose the potential buyer specifies a price range of $200, 000 to $250, 000, and the result of the search returns thousands of homes with prices distributed uniformly throughout that range.
(a) What would be the probability density function that best describes this distribution of housing prices?
Answer:
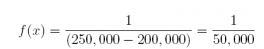
Answer:
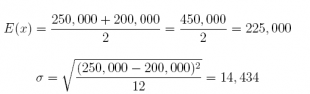
(c) If the buyer ultimately selects a home from this initial list of possibilities, what is the probability she will have to pay more than $235, 000? Use R to find the solution.
Answer: 0.3000.
1 - punif(235000, min = 200000, max = 250000)
## [1] 0.3
2. According to British weather forecasters, the average monthly rainfall in London during the month of June is µ = 2.09 inches. Assume that the average monthly precipitation is a normally distributed random variable with a standard deviation of σ = 0.48 inches. Use R to answer the following questions.
(a) What is the probability that London will have between 1.5 and 2.5 inches of precipitation next June?
Answer: 0.694.
p(1.5 ≤ x ≤ 2.5) = p(−1.23 ≤ z ≤ 0.85) = 0.694
pnorm(2.5, 2.09, 0.48) - pnorm(1.5, 2.09, 0.48)
## [1] 0.693989
(b) What is the probability that London will have an extraordinarily dry month of June with 1 inch or less of precipitation?
Answer: 0.01158
p(x ≤ 1) = p(z ≤ −2.27) = 0.01158
pnorm(1, 2.09, 0.48)
## [1] 0.01157853
(c) If London authorities worry about local flooding when the monthly precipitation falls in the upper 5% of the monthly average, how much rain would London have to receive to cause local authorities to consider preparing for flood conditions?
Answer: 2.88 inches
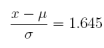
x = µ + (1.645)σ = 2.09 + (1.645)(0.48) = 2.88
qnorm(0.95, 2.09, 0.48)
## [1] 2.87953
3. The time required by students to complete an organic chemistry examination is normally distributed with a mean of µ = 200 minutes and a standard deviation of σ = 20 minutes. Use R to answer all questions.
(a) What is the probability a student will complete the examination in 180 minutes or less?
Answer: 0.1587.
p(x ≤ 180) = p(z ≤ −1) = 0.1587
pnorm(180, 200, 20)
## [1] 0.1586553
(b) What is the probability a student will take between 180 and 220 minutes to complete the examination?
Answer: 0.6827.
p(180 ≤ x ≤ 220) = p(−1 ≤ z ≤ 1) = 0.6827
pnorm(220, 200, 20) - pnorm(180, 200, 20)
## [1] 0.6826895
(c) Since this particular class is a large lecture section of 300 students, and the final examination period lasts 240 minutes, how many students would we expect to submit the completed exam on time?
Answer: approximately 293 students should finish on time.
p(x ≤ 240) = p(z ≤ 2) = 0.9772
pnorm(240, 200, 20)
## [1] 0.9772499
Therefore, (0.9772)(300) ≈ 293.
4. A large agricultural producer in Spain produces melons with diameters that are normally distributed with a mean of µ = 15 centimeters (cm) and a standard deviation of σ = 2 cm. Use R to find the solutions to these questions.
(a) What is the probability a melon will have a diameter of at least 12 cm?
Answer: 0.9332
p(x ≥ 12) = p(z ≥ −1.5) = 0.9332
pnorm(12, 15, 2, lower.tail = FALSE)
## [1] 0.9331928
(b) What is the probability that a randomly selected melon will have a diameter of no less than 12 cm but no more than 16 cm?
Answer: 0.6247.
p(12 ≤ x ≤ 16) = p(−1.5 ≤ z ≤ 0.50) = 0.6247
pnorm(16, 15, 2) - pnorm(12, 15, 2)
## [1] 0.6246553
(c) The producer has an arrangement with several gourmet shops by which it will receive a slightly higher price for melons with a diameter that falls in the top 10%. What is the minimum diameter a melon must have in order to qualify for the higher price?
Answer: 17.56 cm.
Since z = 1.28 cuts off the upper 10% of the standard normal probability distribution, we solve for the corresponding value of x this way:
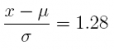
x = µ + (1.28)σ = 15 + (1.28)(2) = 17.56
qnorm(0.90, 15, 2)
## [1] 17.5631
5. The number of visits to the Book4Less.com discount travel website is a Poisson distributed random variable with a mean of 10 visits per minute. Use R to answer all questions.
(a) What is the mean of the associated exponential probability distribution?
Answer: If the mean Poisson arrival rate is 10 visitors per minute (every 60 seconds), then the time between passenger visitors is exponentially distributed with a mean of 6 seconds.
(b) Write out the exponential probability density function f (x).
Answer:
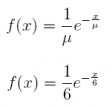
(c) Write out the cumulative probability function.
Answer:
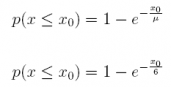
(d) What is the standard deviation σ of the distribution?
(e) If the internet server experiences an 18-second power failure during which time people would be denied access to the website, what is the probability that no one attempted to visit and thus no business was lost during the down-time?
Since we are told that there is an average of 10 visitors per minute, or 10 visitors per 60 seconds, we need to convert this parameter: µ =10 visitors/60 seconds = 3 visitors/18 seconds. What is the Poisson probability of 0 visitors in 18 seconds given that the expected number is 3?
Answer: 0.04979.

dpois(0, 3)
## [1] 0.04978707