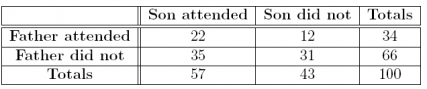
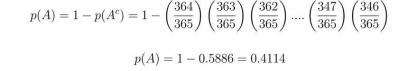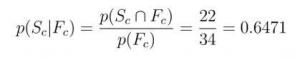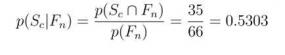Answer:
0.4114. The probability that at least two people (out of 20) share the same birthday is one minus the probability that no one shares the same birthday. Let A be the event that at least two people share the same birthday, and Ac be the event that no one (out of 20) shares the same birthday. Then
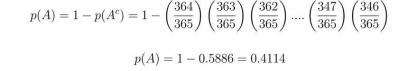
#Comment1. find the probability of event A-complement (probability
#no one shares the same birthday)
probAcomp = ((365)*(364)*(363)*(362)*(361)*(360)*(359)*(358)
*(357)*(356)*(355)*(354)*(353)*(352)*(351)*(350)
*(349)*(348)*(347)*(346)) / ((365) ^ 20)
#Comment2. find probability of event A (at least 2 people share
#same birthday)
probA = 1 - probAcomp
#Comment3. the probability of event A
probA
## [1] 0.4114
#Comment4. a more convenient way to compute probability of event
#A-complement using prod() function
NewprobAcomp = prod(365 : 346) / (365) ^ 20
#Comment5. use NewprobAcomp to find probability of event A
NewprobA = 1 - NewprobAcomp
#Comment6. the probability of event A
NewprobA
## [1] 0.4114384