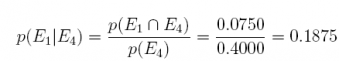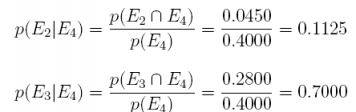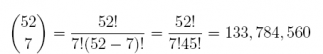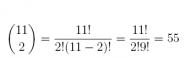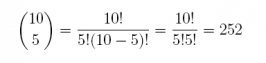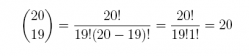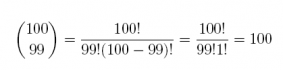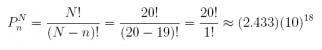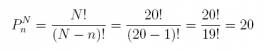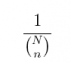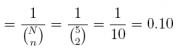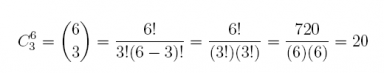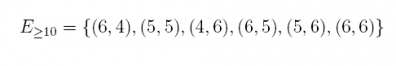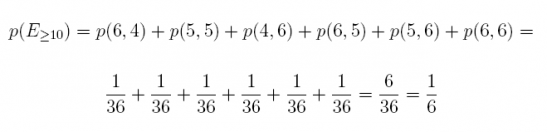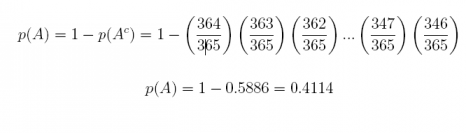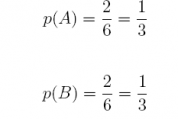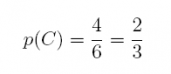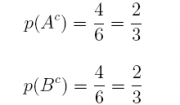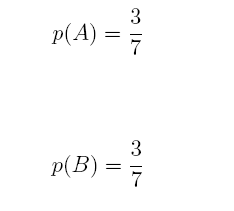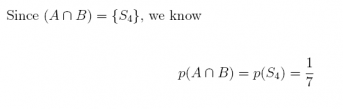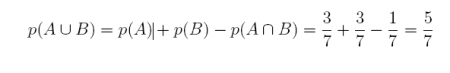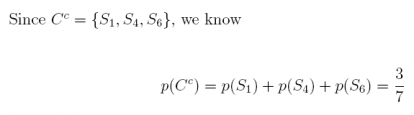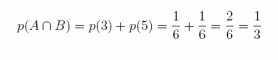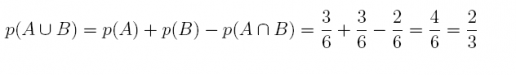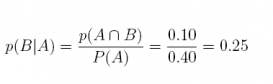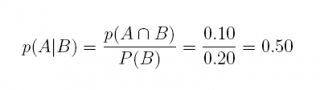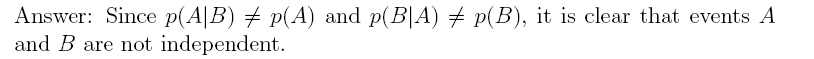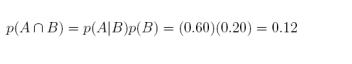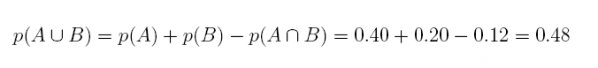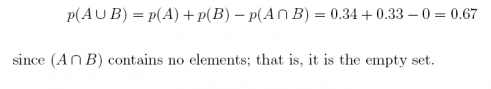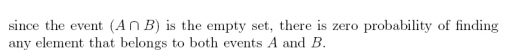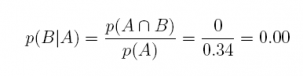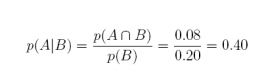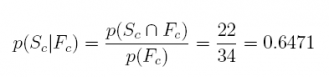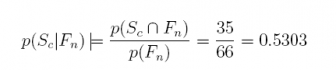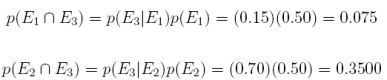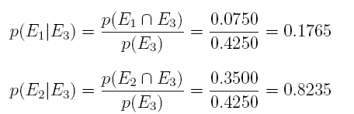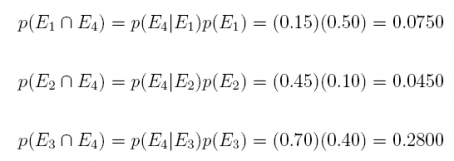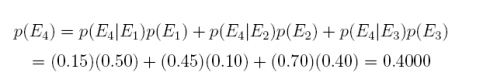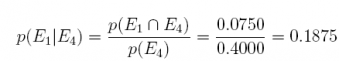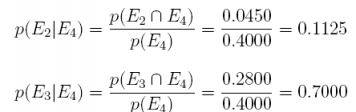1. A two-step experiment consists of fipping a coin (on the first step) and casting a die (on the second). Write out the sample space. How many outcomes are possible?
Answer: Since the experiment has N = 2 steps with n1 = 2 results on the first step and n2 = 6 on the second, there would be
(n1)(n2) = (2)(6) = 12
outcomes for the overall experiment. The sample space is listed below.
S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
#Comment. Use the * multiplication operator.
2 * 6
## [1] 12
2. For a popular version of a card game, 7 cards are dealt from the deck of 52. How many different hands of 7 cards can be drawn from 52?
Answer: Using the Counting Rule for Combinations, and n = 7 from N = 52, there are 133, 784, 560 unique hands of 7 cards from a deck of 52.
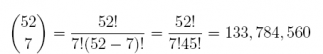
#Comment. Use the function choose(N,n) to find number of
#combinations of N items taken n at a time.
choose(52, 7)
## [1] 133784560
3. The process of drawing cards from deck is known as sampling without replacement because once a card is drawn (and added to a player's hand) it is not replaced in the deck and thus cannot be drawn again. Suppose a new computer-based card game is designed which relaxes this restriction, and allows sampling with replacement, where each card drawn is then returned to the original deck from which it may be drawn again. How many unique hands are possible?
Answer: Applying the Counting Rule for the Multiple-Step Experiment, there are N = 7 steps with n = 52 possible results on each step: (n1) = (n2) = … = (n7) = 52. The number of outcomes for the overall experiment is 1,028,071,702,528 possible unique hands. Note: R reports very large (and very small) numbers using scientifc notation: 1.028072e + 12 is actually 1.028072(10)12. See Comment 1. To see how to express this value in non-scientific notation, see Comment 2.
#Comment1. Use ^ operator to raise a number to a power.
52 ^ 7
## [1] 1.028072e+12
#Comment2. To avoid an answer reported in scientific notation,
#include: options(scipen = 999)
options(scipen = 999)
52 ^ 7
## [1] 1028071702528
4. The number of outcomes when sampling with replacement exceeds the number of outcomes when sampling without replacement. Why?
Answer: The reason why there are so many more possible experimental outcomes in the game with sampling with replacement than with the game with sampling without replacement is that there are many more possible results on each of the 7 steps of the multiple-step experiment. By comparing the first 3 steps in both games, this becomes clear. For the rst game, after 3 steps, there are (52)(52)(52) = 140, 608 possible results whereas for the second game, there are only (52)(51)(50) = 132, 600. As more cards are dealt—the deeper into the experiment one goes—the greater this divergence in the number of possible outcomes.
5. For each problem below, how many ways can n objects can be selected from N?
Answer:
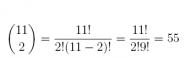
#Comment. Use the choose(N,n) function to find number of
#combinations of N items taken n at a time.
choose(11, 2)
## [1] 55
Answer:
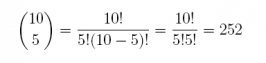
choose(10, 5)
## [1] 252
Answer:
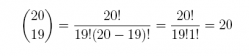
choose(20, 19)
## [1] 20
Answer:
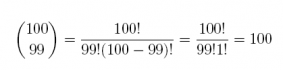
choose(100, 99)
## [1] 100
Answer:
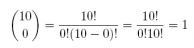
choose(10, 0)
## [1] 1
6. Find the number of permutations of n objects selected from N objects.
Answer:
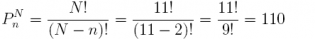
#Comment. Use the ratio of factorials to find the number of
#permutations of N items taken n at a time.
factorial(11) / factorial(11 - 2)
## [1] 110
Answer:
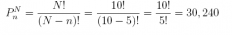
factorial(10) / factorial(10 - 5)
## [1] 30240
Answer:
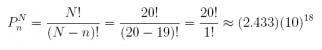
factorial(20) / factorial(20 - 19)
## [1] 2432902008176640000
Answer:
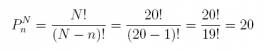
factorial(20) / factorial(20 - 1)
## [1] 20
Answer:
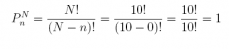
factorial(10) / factorial(10 - 0)
## [1] 1
7. A simple random sample (SRS) of size n drawn from a finite population of size N is a sample that has been chosen such that all possible samples of size n are equally- likely. If one uses an SRS procedure to draw a sample of size n from N, what is the probability of each sample? Note: SRS is covered extensively in Chapter 7.
Answer: If one uses an SRS procedure to select a sample of size n from a finite population of size N, then the probability of any given sample is
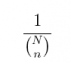
8. Suppose we select a SRS of n = 2 balls from an urn containing a population of N = 5 balls (painted with the letters A, B, C, D , and E). List the sample space of all possible samples or experimental outcomes.
Answer: The sample space S of all possible samples of size n = 2 is
S = {(AB), (AC), (AD), (AE), (BC), (BD), (BE), (CD), (CE), (DE)}
9. Referring to the previous exercise, what is the probability of each possible sample?
Answer: Since there are 10 possible samples, and since SRS requires that each be equally-
likely, the probability of any SRS must be 1/10.
p(AB) = p(AC) = p(AD) = p(AE) = p(BC) = p(BD)
= p(BE) = p(CD) = p(CE) = p(DE) = 0:10
Second, applying the rule from above
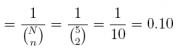
10. Although this rule (used in the preceding two exercises) provides the probability for any SRS of size n selected from a finite population of size N, does it apply when drawing samples from an infnite population?
Answer: The rule does not apply because it is not possible to specify the size of the population N in advance. In fact, the expression could not even be calculated since there is no value for N. This happens when, for example, a sample of items is being selected as they come o an assembly line, or when a sample of customers is being chosen as they depart from a big-box retailer.
11. Suppose we select a SRS of n = 3 balls from an urn containing a population of N = 6 balls (painted with the numbers 1, 2, 3, 4, 5, and 6). List the sample space S of all possible outcomes.
Answer:
S = {(1, 2, 3), (1, 2, 4), (1, 2, 5), (1, 2, 6), (1, 3, 4), (1, 3, 5), (1, 3, 6), (1, 4, 5), (1, 4, 6), (1, 5, 6),
(2, 3, 4), (2, 3, 5), (2, 3, 6), (2, 4, 5), (2, 4, 6), (2, 5, 6), (3, 4, 5), (3, 4, 6), (3, 5, 6), (4, 5, 6)}
12. Referring to the above exercise, how many sample points are there? Use combinations.
Answer:
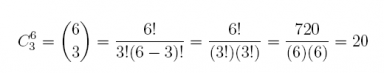
The counting rule confirms that there are 20 possible simple random samples.
choose(6, 3)
## [1] 20
13. Again referring to the above exercise, how many permutations of 3 items can be taken from 6?
Answer: The number of permutations of 3 items taken from 6 is
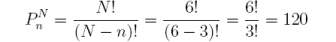
factorial(6) / factorial(6 - 3)
## [1] 120
14. Referring once more to the above exercise, it is clearly impractical (and unnecessary) to list all 120 permutations. It is, however, possible to gain a bit more insight into this issue. List each permutation of the first triple in the answer to above question: (1, 2, 3).
Answer: There are 6 possible ways that (1,2,3) can be ordered. Here they are
(1, 2, 3)(1, 3, 2)(2, 1, 3)(2, 3, 1)(3, 1, 2)(3, 2, 1)
If (1, 2, 3) can be arranged in 6 ways, how many ways can (1, 3, 2) be ordered? Clearly, (1, 3, 2) can also be arranged in 6 ways, and this is true of all 20 combinations. Since each of the 20 combinations can be arranged in 6 di erent ways, there are (20)(6) = 120 permutations.
15. Consider the experiment of rolling a pair of dice. Suppose we are interested in the sum of the face values showing on the dice.
(a) What is the probability of obtaining a value of 3 or less?
Answer: There are 3 different ways the experiment can result in two values summing to 3 or less. Let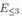 
be the event that the two dice sum to 3 or less.
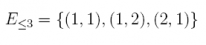
and
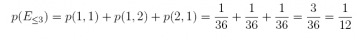
Therefore, there is a 1/12 probability of obtaining a value of 3 or less.
(b) What is the probability of obtaining a value of 10 or more?
Answer: There are 6 different ways the experiment can result in values summing to 10 or more. Let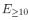 
be the event that the two dice sum to 10 or more.
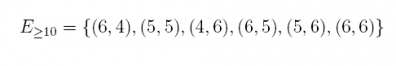
and
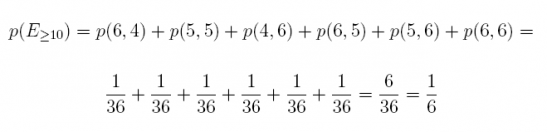
Therefore, there is a 1/6 probability of obtaining a value of 10 or more.
(c) Which of the three methods of assigning probability values has been used?
Answer: the classical method of assigning probabilities has been used because the assumption of equally-likely outcomes seems valid.
16. A class has 20 enrolled students. What is the probability that two or more students have the same birthday? As a simplifying assumption, ignore leap years.
Hint: Recall that the probability of an event A equals one minus the probabilty of the complement of that event, Ac. That is, p(A) = 1 — p(Ac).
Answer: The probability that at least two people (out of 20) share the same birthday is one minus the probability that no one shares the same birthday. Let A be the event at least two people share the same birthday, and Ac be the event that no two people (out of 20) share the same birthday. Then
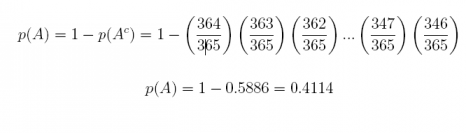
#Comment1. Use * and / operators to find products and ratios.
probAcomp = ((365) * (364) * (363) * (362) * (361) * (360) * (359) * (358) * (357) * (356) * (355) * (354) * (353) * (352) *(351) * (350) * (349) * (348) * (347) * (346)) /((365) ^ 20)
#Comment2. The probability of any event equals one minus the
#probability of the complement of that event.
probA = 1 - probAcomp
#Comment3. Examine contents of probA.
probA
## [1] 0.4114384
#Comment4. Alternatively, use function prod(N:n) to find product
#N*(N-1)*(N-2)*(N-3)*...*(n+2)*(n+1)*(n).
NewprobAcomp = prod(365 : 346) / (365) ^ 20
#Comment5. The probability of any event equals one minus the
#probability of the complement of that event.
NewprobA = 1 - NewprobAcomp
#Comment6. Examine contents of NewprobA. The results are the same.
NewprobA
## [1] 0.4114384
Thus there is a 0.4114 probability that at least 2 people share the same birthday.
17. An experiment consists of casting a single die; the sample space is S = {1, 2, 3, 4, 5, 6} Define 3 events: A = {1, 2}, B = {3, 4}, and C = {2, 3, 5, 6}.
(a) What are p(A), p(B), and p(C)?
Answer:
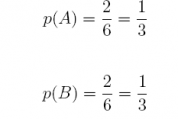
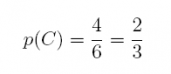
Answer:
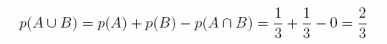
Note that since A and B are mutually exclusive,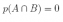 
Answer:
Ac = {3, 4, 5, 6}
Bc = {1, 2, 5, 6}
(d) What is p(Ac)? What is p(Bc)
Answer:
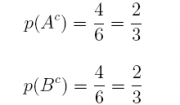
18. Suppose that we have an experiment with the sample space comprised of 7 equally- likely sample points, S = {S1, S2, S3, S4, S5, S6, S7}. De ne 3 events in the following way: A = {S1, S4, S6}, B = {S2, S4, S7}, and C = {S2, S3, S5, S7}
(a) What is p(A), p(B), and p(C)?
Answer:
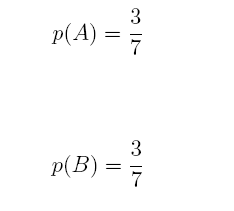
(b) What is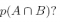 
Answer:
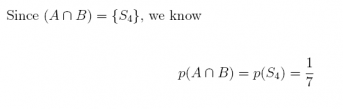
Answer:
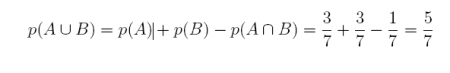
Answer:
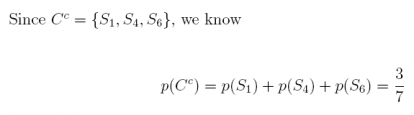
19. An experiment consists of the roll of a single die; the sample space is S = {1, 2, 3, 4, 5, 6}. Define two events: A = {1, 3, 5} and B = {3, 4, 5}.
Answer: (A U B) = {1, 3, 4, 5}
(b) What is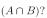
Answer:
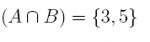
(c) What is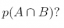 
Answer:
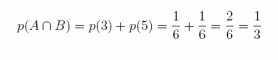
Answer:
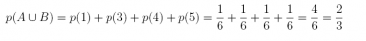
20. Referring to the previous exercise, could we use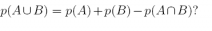 
Answer: Yes, we could.
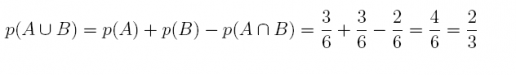
21. Suppose we have two events A and B with p(A) = 0.40 and p(B) = 0.20; the probability of the intersection of these two events is 0.10.
Answer:
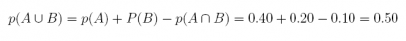
Answer:
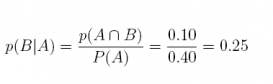
Answer:
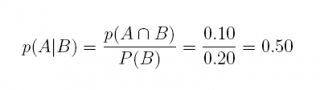
(d) Are events A and B independent?
22. Suppose we have two events A and B with p(A) = 0.40 and p(B) = 0.20; the conditional probability of event A given B is 0.60.
(a) What is the probability of the intersection of events A and B?
Answer:
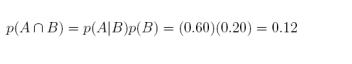
(b) What is the conditional probability of event B given A?
Answer:
(c) What is the probability of the union of events A and B?
Answer:
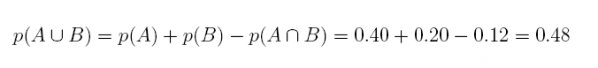
23. Suppose an experiment has three mutually-exclusive events, A, B, and C, with p(A) = 0.34, p(B) = 0.33, and p(C) = 0.33.
(a) What is the probability of the union of events A and B?
Answer:
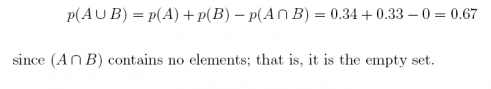
(b) What is the probability of the intersection of events A and B?
Answer:
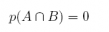
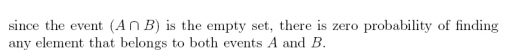
(c) What is the conditional probability of event B given A?
Answer:
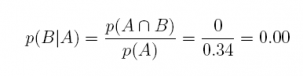
24. Suppose we have two events A and B with p(A) = 0.40 and p(B) = 0.20. Moreover, p(A|B) = p(A) and p(B|A) = p(B).
(a) What is the probability of the intersection of events A and B?
Answer:
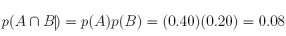
(b) What is the conditional probability of event A given B?
Answer:
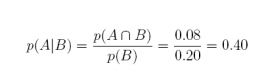
(c) What is the probability of the union of events A and B?
Answer:
25. The following data from a sample of 100 families show the record of college attendance by fathers and their oldest sons: in 22 families, both father and the son attended college; in 31 families, neither father nor son attended college; in 12 families, the father attended college while the son did not; and in 35 families, the son attended college but the father did not.
(a) What is the probability a son attended college given that his father attended college?
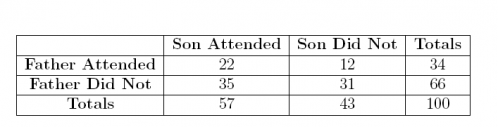
Organizing this information in a simple table
Define the following events
Sc is event that the son attended college
Sn is event that the son did not attend college
Fc is event that the father attended college
Fn is event that the father did not attend college
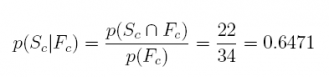
Answer: 0.6471. There is almost a 65% chance that a son attended college given that his father did.
(b) What is the probability a son attended college given that his father did not attend college?
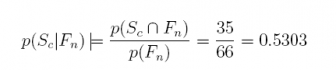
Answer: 0.5303. There is a 53% chance that a son attended college if his father did not.
(c) Is attending college by the son independent of whether his father attended college?
Answer: Since p(Sc|Fc) = 0.6471>p(Sc) = 0.5700, the events are not independent. In other words, knowing whether the father attended college tells us something about whether the son is likely to have attended.
26. We have the following probabilities and events: the prior probabilities for 2 events E1 and E2 are p(E1) = 0.50 and p(E2) = 0.50 and the conditional probilities are p(E3|E1) = 0.15 and p(E3|E2) = 0.70. Summarize this information in a table, and answer the 3 questions below.
Answer: Multiplying the prior probability times the conditional probability
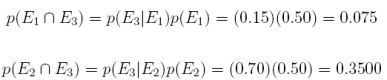
Answer: Summing the two joint probabilities
p(E3) = p(E3|E1)p(E1)+p(E3|E2)p(E2) = (0:15)(0:50)+(0:70)(0:50) = 0:4250
(c) What are p(E1|E3) and p(E2|E3)?
Answer: The divide the joint probabilities by p(E3)
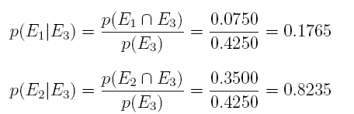
27. Consider the following facts: (a) in random testing, you test positive for a disease; (b) all people who have the disease test positive for it; (c) in 5% of the cases, this test shows positive even when a person does not have the disease (that is, there is a 5% chance of a false positive); and (d) in the population-at-large, one person in a thousand has the disease. What is the probability that you have the disease? Hint: de ne the following events: D is event person has the disease; Dc is event person does not have the disease; P is event person tests positive for the disease.
Answer:
Thus, perhaps surprisingly, even if you test positive for this disease, there is less than a 2% chance that you actually have it.
28. We have the following probabilities and events: the prior probabilities for 3 events E1, E2, and E3 are p(E1) = 0.50, p(E2) = 0.10, and p(E3) = 0.40 and the conditional probabilities are p(E4|E1) = 0:15, p(E4|E2) = 0.45 and p(E4|E3) = 0.70. Summarize this information in a table, and answer the 3 questions below.
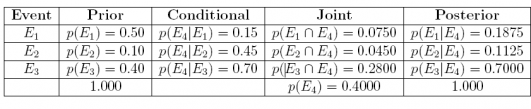
Answer: Multiplying the prior probability times the conditional probability
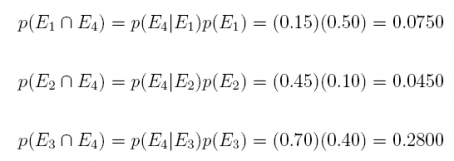
Answer: Summing the three joint probabilities
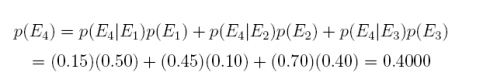
Answer: The divide the joint probabilities by p(E4)
