Chapter 6: Continuous Probability Distributions

1. Let x be the random variable described by the uniform probability distribution with its lower bound at a = 120, upper bound at b = 140.

(a) What is the probability density function, f(x)?

Answer: if a = 120 and b = 140, then

fig

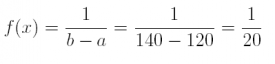
(b) What is E(x) and σ?

Answer: the expected value and standard deviation are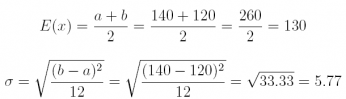 fig

2. What is p(x = 130)? Explain why p(x = 130) ≠ 1/20.

Answer: p(x = 130) = 0, just as it is for any value of x in the interval 120 ≤ x ≤ 140. The probability density function f(x) does not provide probabilities but only the height of the curve above the horizontal axis at a particular value of x. In this case, the height (but not the probability) is 1/20.

3. Referring to the previous exercise, find the following probabilities using f(x) and R.

(a) p(125≤ x ≤ 135)

Answer: 0.5000

fig

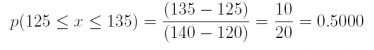
#Comment. Subtract punif(125,min=120,max=140) from
#punif(135,min=120,max=140).
punif(135, min = 120, max = 140) -
punif(125, min = 120, max = 140)

## [1] 0.5

(b) p(125 ≤ x ≤ 131)

Answer: 0.3000

#Comment. Subtract punif(125,min=120,max=140) from
#punif(131,min=120,max=140).
punif(131, min = 120, max = 140) -
punif(125, min = 120, max = 140)
## [1] 0.3

Answer: 0.1000

#Comment. Subtract punif(129,min=120,max=140) from
#punif(131,min=120,max=140).
punif(131, min = 120, max = 140) -
punif(129, min = 120, max = 140)
## [1] 0.1

(d) p(120.50 ≤ x ≤139.50)

Answer: 0.9500

#Comment. Subtract punif(120.50,min=120,max=140) from
#punif(139.50,min=120,max=140).
punif(139.50, min = 120, max = 140) -
punif(120.50, min = 120, max = 140)
## [1] 0.95

4. Referring to the previous exercise, find the following probabilities using f(x) and R.

(a) p(x ≥ 124)

Answer: 0.8000

#Comment1. 1 minus punif(124,min=120,max=140)
1 - punif(124, min = 120, max = 140)
## [1] 0.8
#Comment2. Use punif(124,min=120,max=140,lower.tail=FALSE);
#the argument lower.tail=FALSE results in the upper tail area,
#not the lower tail area (as normally happens with punif()).
punif(124, min = 120, max = 140, lower.tail = FALSE)
## [1] 0.8

(b) p(x ≥ 128)

Answer: 0.6000

#Comment1. 1 minus punif(128,min=120,max=140).
1 - punif(128, min = 120, max = 140)
## [1] 0.6
#Comment2. Use punif(128,min=120,max=140,lower.tail=FALSE).
punif(128, min = 120, max = 140, lower.tail = FALSE)
## [1] 0.6

Answer: 0.3000

#Comment1. 1 minus punif(134,min=120,max=140).
1 - punif(134, min = 120, max = 140)
## [1] 0.3
#Comment2. Use punif(134,min=120,max=140,lower.tail=FALSE).
punif(134, min = 120, max = 140, lower.tail = FALSE)
## [1] 0.3

(d) p(x ≥ 139)

Answer: 0.0500

#Comment1. 1 minus punif(139,min=120,max=140).
1 - punif(139, min = 120, max = 140)
## [1] 0.05
#Comment2. Use punif(139,min=120,max=140,lower.tail=FALSE).
punif(139, min = 120, max = 140, lower.tail = FALSE)
## [1] 0.05

5. A recent college graduate is moving to Houston, Texas to take a new Job, and is looking to purchase a home. Since Greater Houston takes in a relatively large metropolitan area of nearly 7,000,000 people, there are many homes from which to choose. When consulting the real estate web sites, it is possible to select the price range of housing in which one is most interested. Suppose the potential buyer species $200,000 to $250,000, and the result returns 105 homes with prices distributed uniformly throughout that range. Please answer the following questions

(a) What would be the probability density function that best describes this distribution of housing prices?

Answer:

(b) What are E(x) and σ?

Answer:

fig

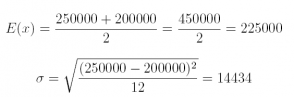
(c) If the buyer ultimately selects a home randomly from this initial list of 105 homes, what is the probability she will have to pay more than $235,000?

Answer: 0.3000

fig

#Comment1. 1 minus punif(235000,min=200000,max=250000).
1 - punif(235000, min = 200000, max = 250000)
## [1] 0.3
#Comment2. Or punif( ,lower.tail=FALSE)
punif(235000, min = 200000, max = 250000, lower.tail = FALSE)
## [1] 0.3

6. Referring to the above question, what is the minimum price the buyer would pay if she refines her focus to the upper 25% of the price range from $200,000 to $250,000? Note that it is possible to omit the min= and max= notation as long as the arguments are placed in the same order; that is, as long as the lower bound is placed first, the upper bound is placed immediately after it.

Answer: $237,500

#Comment1. Use function qunif(0.75,200000,250000) to find that price
#for which 25 percent of listings are higher, 75 percent are lower.
qunif(0.75, 200000, 250000)
## [1] 237500
#Comment2. Use qunif(0.25, 200000, 250000, lower.tail = FALSE)
qunif(0.25, 200000, 250000, lower.tail = FALSE)
## [1] 237500

7. Use R to answer the following questions concerning z, the standard normal variable.

(a) p(z ≤ 2.33)?

Answer: 0.9901. The probability that z is less than or equal to 2.33 is about 0.99.

#Comment. Use function pnorm(2.33) to find the probability
#that z will be less than or equal to 2.33.
pnorm(2.33)
## [1] 0.9900969

(b) p(z ≤ 2.05)?

Answer: 0.9798. The probability that z is less than or equal to 2.05 is about 0.98.

#Comment. Use function pnorm(2.05) to find the probability
#that z will be less than or equal to 2.05.
pnorm(2.05)
## [1] 0.9798178

Answer: 0.9750. The probability that z is less than or equal to 1.96 is about 0.9750.

#Comment. Use function pnorm(1.96) to find the probability
#that z will be less than or equal to 1.96.
pnorm(1.96)
## [1] 0.9750021

(d) p(z ≤ 1.28)?

Answer: 0.8997. The probability that z is less than or equal to 1.28 is about
0.90.

#Comment. Use function pnorm(1.28) to find the probability
#that z will be less than or equal to 1.28.

pnorm(1.28)
## [1] 0.8997274

8. Use R to answer the following questions about z.

(a) p(z ≤ 0.00)?

Answer: 0.5000. The probability that z will be less than or equal to 0.00 is 0.5000.

#Comment. Use function pnorm() to find cumulative probability.
pnorm(0.00)
## [1] 0.5

(b) p(z ≤ –1.28)?

Answer: 0.1003. The probability that z will be less than or equal to -1.28 is about 0.10.

#Comment. Use function pnorm() to find cumulative probability.
pnorm(-1.28)
## [1] 0.1002726

(c) p(z ≤ –1.96)?

Answer: 0.025. The probability that z will be less than or equal to -1.96 is about 0.025.

#Use function pnorm() to find cumulative probability.
pnorm(-1.96)
## [1] 0.0249979

(d) p(z ≤ –2.05)?

Answer: 0.02018. The probability that z will be less than or equal to -2.05 is about 0.02.

#Comment. Use function pnorm() to find cumulative probability.
pnorm(-2.05)
## [1] 0.02018222

(e) p(z ≤ –2.33)?

Answer: 0.009903. The probability that z will be less than or equal to -2.33 is about 0.01.

#Comment. Use function pnorm() to find cumulative probability.
pnorm(-2.33)
## [1] 0.009903076

9. Use R to answer the following questions about z.

(a) p(z ≥ −2.33)

Answer: 0.9901. The probability that z will be greater than or equal to -2.33 is about 0.99.

#Comment1. 1 minus probability z is less than or equal to -2.33.

1 − pnorm(−2.33)

## [1] 0.9900969

#Comment2. Use pnorm(−2.33, lower.tail = FALSE) to confirm.

pnorm(−2.33, lower.tail = FALSE)

## [1] 0.9900969

(b) p(z ≥ −2.05)

Answer: 0.9798. The probability that z will be greater than or equal to −2.05 is about 0.98.

#Comment1. 1 minus probability z is less than or equal to −2.05.

1 − pnorm(−2.05)

## [1] 0.9798178

#Comment2. Use pnorm(−2.05, lower.tail = FALSE) to confirm.

pnorm(−2.05, lower.tail = FALSE)

## [1] 0.9798178

Answer: 0.975. The probability that z will be greater than or equal to −1.96 is about 0.975.

#Comment1. 1 minus probability z is less than or equal to −1.96.

1 - pnorm(-1.96)

## [1] 0.9750021

#Comment2. Use pnorm(-1.96, lower.tail = FALSE) to confirm.

pnorm(-1.96, lower.tail = FALSE)

## [1] 0.9750021

(d) p(z ≥ −1.28)

Answer: 0.8997. The probability that z will be greater than or equal to -1.28 is about 0.90.

#Comment1. 1 minus probability z is less than or equal to -1.28.

1 - pnorm(-1.28)

## [1] 0.8997274

#Comment2. Use pnorm(-1.28, lower.tail = FALSE) to confirm.

pnorm(-1.28, lower.tail = FALSE)

## [1] 0.8997274

10. Use R to answer the following questions about z.

(a) p(z ≥ 1.28)

Answer: 0.1003. The probability that z will be greater than or equal to 1.28 is about 0.10.

#Comment1. 1 minus probability z is less than or equal to 1.28.

1 - pnorm(1.28)

## [1] 0.1002726

#Comment2. Use pnorm(1.28, lower.tail = FALSE) to confirm.

pnorm(1.28, lower.tail = FALSE)

## [1] 0.1002726

(b) p(z ≥ 1.96)

Answer: 0.025. The probability that z will be greater than or equal to 1.96 is about 0.025.

#Comment1. 1 minus probability z is less than or equal to 1.96.

1 - pnorm(1.96)

## [1] 0.0249979

#Comment2. Use pnorm(1.96, lower.tail = FALSE) to confirm.

pnorm(1.96, lower.tail = FALSE)

## [1] 0.0249979

Answer: 0.02018. The probability that z will be greater than or equal to 2.05 is about 0.02.

#Comment. 1 minus probability z is less than or equal to 2.05.

1 - pnorm(2.05)

## [1] 0.02018222

#Comment2. Use pnorm(2.05, lower.tail = FALSE) to confirm.

pnorm(2.05, lower.tail = FALSE)

## [1] 0.02018222

(d) p(z ≥ 2.33)

Answer: 0.009903. The probability that z will be greater than or equal to 2.33 is about 0.01.

#Comment1. 1 minus probability z is less than or equal to 2.33.

1 - pnorm(2.33)

## [1] 0.009903076

#Comment2. Use pnorm(2.33, lower.tail = FALSE) to confirm.

pnorm(2.33, lower.tail = FALSE)

## [1] 0.009903076

11. Use R to answer the following questions about z.

(a) If the area to the left of z is 0.99, what is z?

Answer: z = 2.326

#Comment. Use function qnorm(0.99) to find value of z

#providing an area of 0.99 to its left.

qnorm(0.99)

## [1] 2.326348

(b) If the area to the left of z is 0.975, what is z?

Answer: z = 1.96

#Comment. Use function qnorm(0.975) to find value of z

#providing an area of 0.975 to its left.

qnorm(0.975)

## [1] 1.959964

Answer: z = 1.645

#Comment. Use function qnorm(0.95) to find value of z

#providing an area of 0.95 to its left.

qnorm(0.95)

## [1] 1.644854

(d) If the area to the left of z is 0.90, what is z?

Answer: z = 1.282

#Comment. Use function qnorm(0.90) to find value of z

#providing an area of 0.90 to its left.

qnorm(0.90)

## [1] 1.281552

12. Use R to answer the following questions about z.

(a) If the area to the right of z is 0.10, what is z?

Answer: z = 1.282

#Comment1. Use function qnorm(0.90) to find value of z providing

#an area of 0.90 to the left, or what is the same thing an area

#to the right of 0.10.

qnorm(0.90)

## [1] 1.281552

#Comment2. Use qnorm(0.10,lower.tail=FALSE) to confirm.

qnorm(0.10, lower.tail = FALSE)

## [1] 1.281552

(b) If the area to the right of z is 0.05, what is z?

Answer: z = 1.645

#Comment1. Use function qnorm(0.95) to find value of z providing

#an area of 0.95 to the left, or what is the same thing an area

#to the right of 0.05.

qnorm(0.95)

## [1] 1.644854

#Comment2. Use qnorm(0.05, lower.tail = FALSE) to confirm.

qnorm(0.05, lower.tail = FALSE)

## [1] 1.644854

Answer: z = 1.96

#Comment1. Use function qnorm(0.975) to find z providing

#an area of 0.975 to the left, or what is the same thing an area

#to the right of 0.025.

qnorm(0.975)

## [1] 1.959964

#Comment2. Use qnorm(0.025, lower.tail = FALSE) to confirm.

qnorm(0.025, lower.tail = FALSE)

## [1] 1.959964

(d) If the area to the right of z is 0.01, what is z?

Answer: z = 2.326

#Comment1. Use function qnorm(0.99) to find value of z providing

#an area of 0.99 to the left, or what is the same thing an area

#to the right of 0.01.

qnorm(0.99)

## [1] 2.326348

#Comment2. Use qnorm(0.01, lower.tail = FALSE) to confirm.

qnorm(0.01, lower.tail = FALSE)

## [1] 2.326348

13. Let x be a normally-distributed random variable with a mean µ = 25 and standard deviation σ = 5, answer the following questions.

(a) What is the probability that x will be less than or equal to 35?

Answer: 0.9772

#Comment. Use pnorm(35,25,5) for probability x is less than

#or equal to 35 when distribution has mean of 25 and standard

#devation of 5.

pnorm(35, 25, 5)

## [1] 0.9772499

(b) What is the probability that x will be less than or equal to 32?

Answer: 0.9192

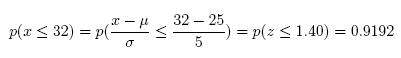
13b_eq1

#Comment. Use pnorm(32,25,5) for probability x is less than

#or equal to 32 when distribution has mean of 25 and standard

#devation of 5.

pnorm(32, 25, 5)

## [1] 0.9192433

Answer: 0.8413

13c_eq1

#Comment. Use pnorm(30,25,5) for probability is less than

#or equal to 30 when distribution has mean of 25 and standard

#devation of 5.

pnorm(30, 25, 5)

## [1] 0.8413447

(d) What is the probability that x will be less than or equal to 25?

Answer: 0.50

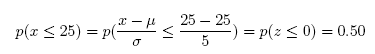
13d_eq1

#Comment. Use pnorm(25,25,5) for probability x is less than

#or equal to 25 when distribution has mean of 25 and standard

#devation of 5.

pnorm(25, 25, 5)

## [1] 0.5

14. If x is a normally-distributed random variable with a mean µ = 63 and standard deviation σ = 4.5, answer the following questions.

(a) What is the probability that x will be less than or equal to -57?

Answer: 0.9088

#Comment. Use pnorm(-57,-63,4.5) for probability x is less than

#or equal to -57 when distribution has mean of -63 and standard

#devation of 4.5.

pnorm(-57, -63, 4.5)

## [1] 0.9087888

(b) What is the probability that x will be less than or equal to -60?

Answer: 0.7475

#Comment. Use pnorm(-60,-63,4.5) for probability x is less than

#or equal to -60 when distribution has mean of -63 and standard

#devation of 4.5.

pnorm(-60, -63, 4.5)

## [1] 0.7475075

Answer: 0.50

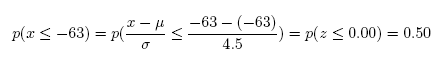
14c_eq1

#Comment. Use pnorm(-63,-63,4.5) for probability x is less than

#or equal to -63 when distribution has mean of -63 and standard

#devation of 4.5.

pnorm(-63, -63, 4.5)

## [1] 0.5

(d) What is the probability that x will be less than or equal to -70?

Answer: 0.05991

14d_eq1

#Comment. Use pnorm(-70,-63,4.5) for probability x is less than

#or equal to -70 when distribution has mean of -63 and standard

#devation of 4.5.

pnorm(-70, -63, 4.5)

## [1] 0.05990691

15. If x is a normally-distributed random variable with a mean µ = 36 and standard deviation σ = 3, answer the following questions.

(a) What is the probability that x will be greater than 42?

Answer: 0.02275

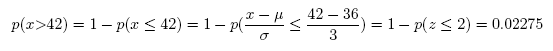
15a_eq1

#Comment1. 1 minus probability x is less than or equal to 42

#when distribution has mean of 36 and standard deviation of 3.

1 - pnorm(42, 36, 3)

## [1] 0.02275013

#Comment2. Use pnorm(42,36,3,lower.tail=FALSE) to confirm.

pnorm(42, 36, 3, lower.tail = FALSE)

## [1] 0.02275013

(b) What is the probability that x will be greater than 39?

Answer: 0.1587

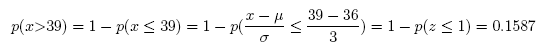
15b_eq1

#Comment1. 1 minus probability x is less than or equal to 39

#when distribution has mean of 36 and standard deviation of 3.

1 - pnorm(39, 36, 3)

## [1] 0.1586553

#Comment2. Use pnorm(42,36,3,lower.tail=FALSE) to confirm.

pnorm(39, 36, 3, lower.tail = FALSE)

## [1] 0.1586553

Answer: 0.8413

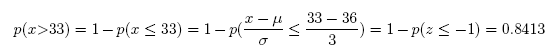
15c_eq1

#Comment1. 1 minus probability x is less than or equal to 33

#when distribution has mean of 36 and standard deviation of 3.

1 - pnorm(33, 36, 3)

## [1] 0.8413447

#Comment2. Use pnorm(33,36,3,lower.tail=FALSE) to confirm.

pnorm(33, 36, 3, lower.tail = FALSE)

## [1] 0.8413447

(d) What is the probability that x will be greater than 27?

Answer: 0.9987

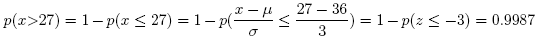
15d_eq1

#Comment1. 1 minus probability x is less than or equal to 27

#when distribution has mean of 36 and standard deviation of 3.

1 - pnorm(27, 36, 3)

## [1] 0.9986501

#Comment2. Use pnorm(27,36,3,lower.tail=FALSE) to confirm.

pnorm(27, 36, 3, lower.tail = FALSE)

## [1] 0.9986501

16. Let x be a normally-distributed random variable with a mean of µ = 100 and a standard deviation of σ = 15.

(a) If the area to the left of x is 0.99, what is x?

Answer: x = 134.9

Method 1. Recall

and the area to the left of z is 0.99 when

z = 2.326

Substituting and solving for x

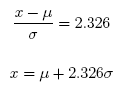
16a_eq3

Plugging in values for the mean and standard deviation µ = 100 and σ = 15

x = µ + 2.326σ = 100 + (2.326)(15) = 100 + 34.89 = 134.9

Method 2. Use R.

#Comment1. Use qnorm(0.99,100,15) to find value of x providing

#area of 0.99 to left with mean 100 and standard deviation 15.

qnorm(.99, 100, 15)

## [1] 134.8952

#Comment2. Use qnorm(0.01,100,15,lower.tail=FALSE) to confirm.

qnorm(0.01, 100, 15, lower.tail = FALSE)

## [1] 134.8952

(b) If the area to the left of x is 0.975, what is x?

Answer: x = 129.4

#Comment1. Use qnorm(0.975,100,15) to find value of x providing

#area of 0.975 to left with mean 100 and standard deviation 15.

qnorm(.975, 100, 15)

## [1] 129.3995

#Comment2. Use qnorm(0.025,100,15,lower.tail=FALSE) to confirm.

qnorm(0.025, 100, 15, lower.tail = FALSE)

## [1] 129.3995

Answer: x = 124.7

#Comment1. Use qnorm(0.95,100,15) to find value of x providing

#area of 0.95 to left with mean 100 and standard deviation 15.

qnorm(.95, 100, 15)

## [1] 124.6728

#Comment2. Use qnorm(0.05,100,15,lower.tail=FALSE) to confirm.

qnorm(0.05, 100, 15, lower.tail = FALSE)

## [1] 124.6728

(d) If the area to the left of x is 0.90, what is x?

Answer: x = 119.20

#Comment1. Use qnorm(0.90,100,15) to find value of x providing

#area of 0.90 to left with mean 100 and standard deviation 15.

qnorm(.90, 100, 15)

## [1] 119.2233

#Comment2. Use qnorm(0.10,100,15,lower.tail=FALSE) to confirm.

qnorm(0.10, 100, 15, lower.tail = FALSE)

## [1] 119.2233

17. Let x be a normally-distributed random variable with a mean of µ = −280 and a standard deviation of σ = 35.

(a) If the area to the right of x is 0.10, what is x?

Answer: x = −235.1

Method 1. Recall

and the area to the right of x is 0.10 when

z = 1.28

Substituting and solving for x

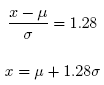
17a_eq2

Plugging in the values for the mean and standard deviation µ = −280 and σ = 35

x = µ + 1.28σ = −280 + (1.28)(35) = −280 + 44.8 = −235.1

Method 2. Use R.

#Comment1. Use qnorm(0.90,-280,35) to find value of x providing

#area of 0.90 to left with mean -280 and standard deviation 35.

qnorm(0.90, -280, 35)

## [1] -235.1457

#Comment2. Use qnorm(0.10,-280,35,lower.tail=FALSE) to confirm.

qnorm(0.10, -280, 35, lower.tail = FALSE)

## [1] -235.1457

(b) If the area to the right of x is 0.05, what is x?

Answer: x = −222.4

#Comment1. Use qnorm(0.95,-280,35) to find value of x providing

#area of 0.95 to left with mean -280 and standard deviation 35.

qnorm(0.95, -280, 35)

## [1] −222.4301

#Comment2. Use qnorm(0.05,-280,35,lower.tail=FALSE) to confirm.

qnorm(0.05, −280, 35, lower.tail = FALSE)

## [1] −222.4301

Answer: x = −211.4

#Comment1. Use qnorm(0.975,-280,35) to find value of x providing

#area of 0.975 to left with mean -280 and standard deviation 35.

qnorm(0.975, -280, 35)

## [1] -211.4013

#Comment2. Use qnorm(0.025,-280,35,lower.tail=FALSE) to confirm.

qnorm(0.025, -280, 35, lower.tail = FALSE)

## [1] -211.4013

(d) If the area to the right of x is 0.01, what is x?

Answer: x = −198.6

#Comment1. Use qnorm(0.99,-280,35) to find value of x providing

#area of 0.99 to left with mean -280 and standard deviation 35.

qnorm(0.99, -280, 35)

## [1] -198.5778

#Comment2. Use qnorm(0.01,-280,35,lower.tail=FALSE) to confirm.

qnorm(0.01, -280, 35, lower.tail = FALSE)

## [1] -198.5778

18. According to British weather forecasters, the average monthly rainfall in London during the month of June is µ = 2.09 inches. Assume the monthly precipitation is a normally-distributed random variable with a standard deviation of σ = 0.48 inches.

(a) What is the probability that London will have between 1.5 and 2.5 inches of precipitation next June?

Answer: 0.694

#Comment. pnorm(2.5,2.09,0.48) less pnorm(1.5,2.09,0.48)

pnorm(2.5, 2.09, 0.48) - pnorm(1.5, 2.09, 0.48)

## [1] 0.693989

(b) What is the probability that London will have 1 inch or less of precipitation?

Answer: 0.01158

#Comment. Use pnorm(1,2.09,0.48) to find probability.

pnorm(1, 2.09, 0.48)

## [1] 0.01157853

(c) If London authorities prepare for flood conditions when the monthly precipitation falls in the upper 5% of the normal June amounts, how much rain would have to fall to cause local authorities to begin flood preparations?

Answer: x = 2.88

Since z = 1.645 cuts off the upper 5% of the standard normal probability distribution, we solve for the corresponding value of x

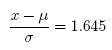
18c_eq1

x = µ + (1.645)σ = 2.09 + (1.645)(0.48) = 2.09 + 0.79 = 2.88

#Comment1. Use qnorm(0.95,2.09,0.48) to find x providing area of 0.95 to left with mean 2.09 and standard deviation 0.48

qnorm(.95, 2.09, 0.48)

## [1] 2.87953

#Comment2. Use qnorm(0.05,2.09,0.48,lower.tail=FALSE) to confirm

qnorm(0.05, 2.09, 0.48, lower.tail = FALSE)

## [1] 2.87953

19. The time required by students enrolled in a pre-medical program to complete an organic chemistry final examination is normally-distributed with a mean of µ = 200 minutes and standard deviation of σ = 20 minutes.

(a) What is the probability a student will complete the examination in 180 minutes or less?

Answer: 0.1587

#Comment. Use pnorm(180,200,20) to find probability.

pnorm(180, 200, 20)

## [1] 0.1586553

(b) What is the probability a student will take between 180 and 220 minutes to complete the examination?

Answer: 0.6827

#Comment. Subtract pnorm(180,200,20) from pnorm(220,200,20).

pnorm(220, 200, 20) - pnorm(180, 200, 20)

## [1] 0.6826895

(c) Since this particular class is a large lecture section of 300 students, and the final examination period lasts 240 minutes, how many students would we expect to submit the completed exam on time?

Answer: Around 293 to 294 students should finish on time.

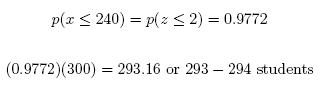
19c_eq1

pnorm(240, 200, 20) * 300

## [1] 293.175

20. A large commerical agricultural concern in Spain produces melons with a diameter that is normally-distributed with a mean of µ = 15 centimeters (cm) and a standard deviation of σ = 2 cm.

(a) What is the probability that a melon will have a diameter of at least 12 cm?

Answer: 0.9332

#Comment1. Use 1 minus pnorm(12,15,2) to find probability.

1 - pnorm(12, 15, 2)

## [1] 0.9331928

#Comment2. Use pnorm(12,15,2,lower.tail=FALSE) to confirm.

pnorm(12, 15, 2, lower.tail = FALSE)

## [1] 0.9331928

(b) What is the probability that a randomly selected melon will have a diameter of no less than 12 cm but no more than 16 cm?

Answer: 0.6247

#Comment. Subtract pnorm(12,15,2) from pnorm(16,15,2).

pnorm(16, 15, 2) - pnorm(12, 15, 2)

## [1] 0.6246553

(c) The producer has an arrangement with one retailer by which they receive a slightly higher price for melons with a diameter falling in the top 10%. What is the minimum diameter a melon must have in order to qualify for the higher price?

Answer: x = 17.56 cm

Since z = 1.28 cuts off the upper 10% of the standard normal probability distribution, we solve for the corresponding value of x

x = µ + (1.28)σ = 15 + (1.28)(2) = 15 + 2.56 = 17.56

Use R to confirm that a melon with a diameter of 17.56 cm sets the cut-off point for the top 10%.

#Comment1. Use qnorm(.90,15,2) to find value of x providing area of 0.90 to left with mean 15 and standard deviation 2.

qnorm(.90, 15, 2)

## [1] 17.5631

#Comment2. Use qnorm(0.10,15,2,lower.tail=FALSE) to confirm.

qnorm(0.10, 15, 2, lower.tail = FALSE)

## [1] 17.5631

21. A variable is exponentially-distributed with a mean of µ = 5.

(a) What is the form of the probability density function?

Answer:

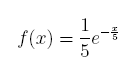
21a_eq1

(b) What is the cumulative probability function?

Answer:

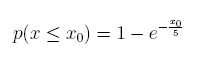
21b_eq1

Answer: 0.3297

#Comment. Use pexp(2,1/5) to find probability x is less than or equal to 2 when the mean is 5.

pexp(2,1/5)

## [1] 0.32968

(d) What is p(x ≤ 4)?

Answer: 0.5507

#Comment. Use pexp(4,1/5) to find probability x is less than

#or equal to 4 when the mean is 5.

pexp(4, 1/5)

## [1] 0.550671

(e) What is p(x ≤ 5)?

Answer: 0.6321

#Comment. Use pexp(5,1/5) to find probability x is less than

#or equal to 5 when the mean is 5.

pexp(5,1/5)

## [1] 0.6321206

(f) What is p(x ≤ 8)?

Answer: 0.7981

#Comment. Use pexp(8,1/5) to find probability x is less than

#or equal to 8 when the mean is 5.

pexp(8,1/5)

## [1] 0.7981035

(g) What is p(x ≤ 15)?

Answer: 0.9502

#Comment. Use pexp(15,1/5) to find probability x is less than

#or equal to 15 when the mean is 5.

pexp(15, 1/5)

## [1] 0.9502129

22. Referring to the preceding exercise, answer the following questions.

(a) What is p(x ≥ 2)?

Answer: 0.6703

#Comment1. 1 minus probability x is less than or equal to 2 when the mean is 5.

1 - pexp(2, 1/5)

## [1] 0.67032

#Comment2. Use pexp(2,1/5,lower.tail=FALSE) to confirm.

pexp(2, 1/5, lower.tail = FALSE)

## [1] 0.67032

(b) What is p(x ≥ 4)?

Answer: 0.4493

#Comment1. 1 minus probability x is less than or equal to 4 when the mean is 5.

1 - pexp(4,1/5)

## [1] 0.449329

#Comment2. Use pexp(4,1/5,lower.tail = FALSE) to confirm.

pexp(4, 1/5, lower.tail = FALSE)

## [1] 0.449329

Answer: 0.3679

#Comment1. 1 minus probability x is less than or equal to 5 when the mean is 5.

1 - pexp(5, 1/5)

## [1] 0.3678794

#Comment2. Use pexp(5,1/5,lower.tail=FALSE) to confirm.

pexp(5, 1/5, lower.tail = FALSE)

## [1] 0.3678794

(d) What is p(x ≥ 8)?

Answer: 0.2019

#Comment1. 1 minus probability x is less than or equal to 8

#when the mean is 5.

1 - pexp(8, 1/5)

## [1] 0.2018965

#Comment2. Use pexp(8,1/5,lower.tail=FALSE) to confirm.

pexp(8, 1/5, lower.tail = FALSE)

## [1] 0.2018965

(e) What is p(x ≥ 15)?

Answer: 0.04979

#Comment1. 1 minus probability x is less than or equal to 15

#when the mean is 5.

1 - pexp(15, 1/5)

## [1] 0.04978707

#Comment2. Use pexp(15,1/5,lower.tail=FALSE) to confirm.

pexp(15, 1/5, lower.tail = FALSE)

## [1] 0.04978707

23. Referring to the previous exercise, answer the following questions.

(a) What is p(2 ≤ x ≤ 4)?

Answer: 0.221

#Comment. Subtract pexp(2,1/5) from pexp(4,1/5).

pexp(4, 1/5) - pexp(2, 1/5)

## [1] 0.2209911

(b) What is p(2 ≤ x ≤ 5)?

Answer: 0.3024

#Comment. Subtract pexp(2,1/5) from pexp(5,1/5).

pexp(5, 1/5) - pexp(2, 1/5)

## [1] 0.3024406

Answer: 0.4684

#Comment. Subtract pexp(2,1/5) from pexp(8,1/5).

pexp(8, 1/5) - pexp(2, 1/5)

## [1] 0.4684235

(d) What is p(2 ≤ x ≤ 15)?

Answer: 0.6205

#Comment. Subtract pexp(2,1/5) from pexp(15,1/5).

pexp(15, 1/5) - pexp(2, 1/5)

## [1] 0.620533

24. The number of visits to the Book4Less.com discount travel website is a Poisson- distributed random variable with a mean arrival rate of 10 visits per minute.

(a) If the Poisson arrival rate is 10 visitors per minute, what is the mean of the associated exponential probility density function?

Answer: If the mean Poisson arrival rate is 10 visitors per minute (every 60 seconds), then the time between passenger visitors is exponentially-distributed with a mean of 6 seconds.

(b) What is the exponential probability density function?

Answer:

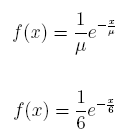
24b_eq1

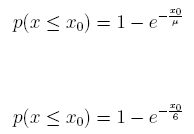
(d) What is the standard deviation of the distribution?

Answer:

σ = µ = 6

25. Referring to the preceding exercise, answer the following questions.

(a) If the internet server experiences a brief power failure of 18 seconds duration during which time people would be denied access to the website, what is the probability that no one attempted to visit the Book4Less.com website anyway and thus no business was lost during the down-time? Use the exponential framework to answer this question.

Answer: 0.04979

#Comment. 1 minus pexp(18,1/6).

1 - pexp(18, 1/6)

## [1] 0.04978707

(b) Answer question (a) using the Poisson probability approach. Confirm that the answer is equal to that in (a).

Answer: 0.04979

Since we are told that there is an average of 10 visitors per minute, or 10 visitors per 60 seconds, we need to convert this parameter: µ=10 visitors/60 seconds=3 visitors/18 seconds.

Recall that the Poisson probability function is

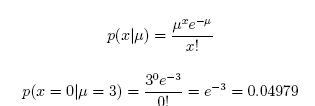
25b_eq1

#Comment. Use dpois(0,3) to find probability of 0 visitors during a period (18 seconds) when the mean is 3 visitors.

dpois(0, 3)

## [1] 0.04978707

(c) Comment on the fact that the answers to parts (a) and (b) are exactly the same regardless of the approach (Poisson or exponential) employed.

Answer: If the interval of time (or distance) between occurrences is distributed exponentially, then the number of occurrences in that interval must be Poisson- distributed. The two distributions are inter-related.

Statistics with R

Student Resources

Chapter 6: Continuous Probability Distributions

(c) p(z ≤ –1.96)?