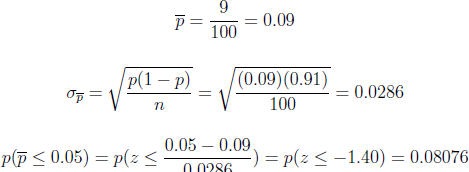1. Draw a random sample of n = 9 from the tv_hours data set (located on the companion website). Apply function data[sample(nrow(data),n ),]. Assign the values to the object named E7_1.
(a) List 9 elements of the random sample taken from the data set.
Answer:
#Comment1. Use function tv_hours[sample(nrow(tv_hours),9),] to
#select a random sample of n=9 from tv_hours and name it E7_1.
E7_1 <– tv_hours[sample(nrow(tv_hours), 9), ]
#Comment2. Examine the contents of E7_1.
E7_1
## [1] 17.75 6.38 11.64 10.25 14.40 16.30 13.42 12.22 9.70
(b) Using this sample, what is the point estimate of the population mean µ?
Answer:
#Comment. Use function mean() to find the sample mean.
mean(E7_1)
## [1] 12.45111
(c) What is the point estimate of the population standard deviation σ?
Answer:
#Comment. Use function sd() to find sample standard deviation.
sd(E7_1)
## [1] 3.49307
2. Draw a second random sample of n = 9. Use data[sample(nrow(data),n),]. Assign the values to the object named E7_2.
(a) List 9 elements of the random sample.
Answer:
#Comment1. Use function tv_hours[sample(nrow(tv_hours),9),] to
#select a random sample of n=9 from tv.hours and name it E7_2.
E7_2 <– tv_hours[sample(nrow(tv_hours), 9), ]
#Comment2. Exam the contents of E7_2.
E7_2
## [1] 17.37 12.63 7.30 11.19 10.48 12.97 17.75 15.79 11.79
(b) Using this sample, what is the point estimate of the population mean µ?
Answer:
#Comment. Use function mean() to find the sample mean.
mean(E7_2)
## [1] 13.03
(c) What is the point estimate of the population standard deviation?
Answer:
#Comment. Use function sd() to find sample standard deviation.
sd(E7_2)
## [1] 3.412364
3. Assuming that the tv_hours data set includes the entire population of interest, what is the population mean? Do the two point estimates (from the two random samples above) equal the population mean? Do they equal one another?
Answer: In general, point estimates do not equal the population parameter they are intended to estimate because they are derived from samples that do not include all the elements of the population; nor can point estimates formed on di erent samples be expected to equal one another.
#Comment1. The mean of the first random sample, E7_1.
mean(E7_1)
## [1] 12.45111
#Comment2. The mean of the second random sample, E7_2.
mean(E7_2)
## [1] 13.03
#Comment3. The mean of the population from tv_hours.
mean(tv_hours$hours)
## [1] 11.6397
4. Referring to E7_1, E7_2, and the tv_hours data set, answer the following questions.
(a) Assuming tv hours includes data on the entire population of interest, what is the population mean µ? Recall that the relevant variable name is hours.
Answer:
#Comment1. Use mean() for mean of entire population.
mean(tv_hours$hours)
## [1] 11.6397
(b) What is the sampling error 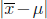 for both random samples (that is, from both E7_1 and E7_2)?
for both random samples (that is, from both E7_1 and E7_2)?
Answer:
#Comment1. Find the absolute value of the difference between
#the sample mean of E7_1 and the population mean.
abs(mean(E7_1)–mean(tv_hours$hours))
## [1] 0.8114111
#Comment2. Find the absolute value of the difference between
#the sample mean of E7_2 and the population mean.
abs(mean(E7_2)–mean(tv_hours$hours))
## [1] 1.3903
5. During the 2012 U.S. Presidential Election, 1,500 voters were interviewed upon exiting from a Manhattan polling station where they had just cast their votes. (The data set is named exit and is available on the companion website.) The data are recorded as a 1 for a Barack Obama vote and a 0 for a Mitt Romney vote. Draw a random sample of n = 25. Apply function data[sample(nrow(data),n),]; assign the values to the object named E7_3.
(a) List the 25 elements of the random sample taken from exit.
Anwer:
#Comment1. Use function exit[sample(nrow(exit),25),] to select
#a random sample of n=25 from exit and name it E7_3.
E7_3 <- exit[sample(nrow(exit), 25), ]
#Comment2. Examine contents of E7_3.
E7_3
## [1] 1 0 1 0 0 1 0 0 1 1 1 0 0 1 0 0 0 0 1 1 1 1 0 1 0
(b) Using this random sample, what is the point estimate of the population proportion p of Obama voters?
Answer:
#Comment. Use function mean() to find the sample proportion.
mean(E7_3)
## [1] 0.48
6. Draw a second random sample of n = 25 from exit and assign the values to the object named E7_4. (Remember: be sure to use the data[sample(nrow(data),n),] function.)
(a) List the 25 elements of the random sample taken from exit.
Answer:
#Comment1. Use function exit[sample(nrow(exit),25),] to select
#a random sample of n=25 from exit and name it E7_4.
E7_4 <– exit[sample(nrow(exit), 25), ]
#Comment2. Examine the contents of E7_4.
E7_4
## [1] 0 0 0 1 0 0 1 0 0 0 1 1 1 0 1 1 1 1 0 0 0 1 1 1 1
(b) Using this random sample, what is the point estimate of the population proportion p of Obama voters?
Answer:
#Comment. Use function mean() to find the sample proportion.
mean(E7_4)
## [1] 0.52
7. Do the two point estimates (found in the preceding two exercises) equal the population proportion? Do they equal one another?
Answer: In general, point estimates do not equal the population parameter they are intended to estimate because they are derived from samples that do not include all the elements of the population; nor can point estimates formed on different samples be expected to equal one another. What is true for sample means is also true for sample proportions.
#Comment1. The proportion of the first random sample, E7_3.
mean(E7_3)
## [1] 0.48
#Comment2. The proportion of the second random sample, E7_4.
mean(E7_4)
## [1] 0.52
#Comment3. The proportion of the population from exit.
mean(exit$obama)
## [1] 0.62
8. How many votes did each candidate receive from those in this sample of n = 1, 500
Answer: Of the 1, 500 voters in sample, Obama received 930 votes, Romney 570.
#Comment. Use the table() function to provide counts of 0 and 1.
table(exit)
## exit
## 0 1
## 570 930
9. Suppose a random sample consists of the following 12 elements: 37, 14, 54, 91, 13, 88, 4, 16, 62, 18, 88, and 99. Copy and paste these values into the R Console and store them in an object named E7_5. Once this has been done, add the variable name values and create a data frame named E7_6. Answer the following questions using E7_6. (This exercise is intended to provide a bit of review of material covered earlier.)
(a) What is the point estimate of the population mean µ?
Answer: 

#Comment1. Use c() function to create the object E7_5.
E7_5 <- c(37, 14, 54, 91, 13, 88, 4, 16, 62, 18, 88, 99)
#Comment2. Examine contents of E7_5.
E7_5
## [1] 37 14 54 91 13 88 4 16 62 18 88 99
#Comment3. Use data.frame() function to create the data frame
#named E7_6. The variable name is values.
E7_6 <- data.frame(values = E7_5)
#Comment4. Examine the contents of E7_6.
E7_6
## values
## 1 37
## 2 14
## 3 54
## 4 91
## 5 13
## 6 88
## 7 4
## 8 16
## 9 62
## 10 18
## 11 88
## 12 99
#Comment5. What is the point estimate of the population mean?
mean(E7_6$values)
## [1] 48.66667
(b) What is the point estimate of the population standard deviation σ?
Answer: s = 35.98

#Comment. Use sd() to calculate the sample standard deviation.
sd(E7_6$values)
## [1] 35.97811
10. When an Iberian tourism authority wanted to know from where travelers on one of their superhighways were coming, they monitored the bridge traffic connecting Castro Marim, Portugal with Ayamonte, Spain (crossing the River Guadiana). They found that for a random sample of 1,062 vehicles, 377 had Portuguese license plates while 418 had Spanish plates. The remaining 267 vehicles had plates from a country other than Spain or Portugal.
(a) What is the point estimate of the population proportion p from Portugal?
Answer: 

(b) What is the point estimate of the population proportion p from Spain?
Answer: 

(c) What is the point estimate of the population proportion p from countries other than Portugal and Spain?
Answer: 

11. A random sample of size n = 36 is drawn from a population with a mean of µ = –17 and a standard deviation of σ = 6.
(a) What is 
Answer: 0.8413

#Comment. Use function pnorm(-16,-17,6/sqrt(36)).
pnorm(-16, -17, 6 / sqrt(36))
## [1] 0.8413447
(b) What is 
Answer: 0.9772

#Comment. 1 minus pnorm(-19,-17,6/sqrt(36)).
1 - pnorm(-19, -17, 6 / sqrt(36))
## [1] 0.9772499
(c) What is 
Answer: 0.6827

#Comment. Subtract pnorm(-18,-17,6/sqrt(36)) from
#pnorm(-16,-17,6/sqrt(36))
pnorm(-16, -17, 6 / sqrt(36)) – pnorm(-18, -17, 6 / sqrt(36))
## [1] 0.6826895
(d) What is 
Answer: 0.9545

#Comment. Subtract pnorm(-19,-17,6/sqrt(36)) from
#pnorm(-15,-17,6/sqrt(36)).
pnorm(-15, -17, 6 / sqrt(36)) - pnorm(-19, -17, 6 / sqrt(36))
## [1] 0.9544997
12. Suppose the mean level of debt carried by students graduating from U.S. universi- ties has now reached $27, 000. Use this value as the population mean µ and assume that the population standard deviation is σ = $4, 500. If a random sample of size n = 121 is selected, answer the following questions.
(a) What is the probability that the sample mean x̄ will fall within ± $500 of the population mean µ? That is, what is p(26500 ≤ x̄ ≤ 27500)?
Answer: 0.7784

#Comment. Subtract pnorm(26500,27000,4500/sqrt(121) from
#pnorm(27500,27000,4500/sqrt(121)
pnorm(27500, 27000, 4500 / sqrt(121)) - pnorm(26500, 27000, 4500 / sqrt(121))
## [1] 0.7783764
(b) What is the probability that the sample mean x̄ will fall within ± $250 of the population mean µ? That is, what is p(26750 ≤ x̄ ≤ 27250)?
Answer: 0.4589

#Comment. Subtract pnorm(26750,27000,4500/sqrt(121) from
#pnorm(27250,27000,4500/sqrt(121)
pnorm(27250, 27000, 4500 / sqrt(121)) - pnorm(26750, 27000, 4500 / sqrt(121))
## [1] 0.458874
13. The provost at a large private university in the U.S. wishes to estimate the mean age for its 3,700 faculty members, and decides to draw a random sample of size n = 37 to derive the sample mean x̄.
(a) Should the nite population correction factor be used in the computation of the standard error of the mean σx?
Answer: No, since 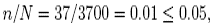 the nite population correction factor is unnecessary.
the nite population correction factor is unnecessary.
(b) Calculate the standard error of the mean both with and without the finite population correction factor. Assume the population standard deviation is σ = 11.1 years. How far apart are the two values?
Answer:


Introducing the finite population correction factor reduces the value of σx̄ by less than one-half of one percent. Clearly, when the size of the sample is small relative to the size of the population, the inclusion of this term makes almost no difference.
14. A study reports that teenagers spend an average of 31 hours a week online and tex- ting. Assume that this is the population mean µ. Assume also that the population standard deviation is σ = 7 hours.
(a) If an random sample of size n = 64 is selected, what is the probability that x̄ is no more than 30? That is, what is p(x̄ ≤ 30)?
Answer: 0.1265

#Comment. Use pnorm(30,31,7/sqrt(64))
pnorm(30, 31, 7 / sqrt(64))
## [1] 0.126549
(b) What is the probability that x̄ is greater than 33? That is, what is p(x̄>33)?
Answer: 0.01114

#Comment. 1 minus pnorm(33,31,7/sqrt(64))
1 - pnorm(33, 31, 7 / sqrt(64))
## [1] 0.01113549
(c) What is the probability x̄ will fall in the interval from 30 to 33 hours? That is, what is p(30 ≤ x̄ ≤ 33)
Answer: 0.8623

#Comment. Subtract pnorm(30,31,7/sqrt(64))
#from pnorm(33,31,7/sqrt(64)).
pnorm(33, 31, 7 / sqrt(64)) - pnorm(30, 31, 7 / sqrt(64))
## [1] 0.8623156
15. Referring to the previous exercise, would it be appropriate to include the finite population correction factor? Are there are circumstances where we might include it?
Answer: No, we would not use the finite population correction factor. The reason is that although we cannot calculate the ratio n/N (because we do not know the size of N ), we can assume that N is very large. Would we ever introduce the term in this question? Yes, if the population were defined as the population of all students at the local high school and if N ≤ 1, 280. As we know, the decision to include the term depends on the ratio of the size of the sample n to the size of the population N .
16. Suppose that in a study of faculty salaries at US-based graduate schools of management, the standard error of the mean is σx̄ = $75 but the population standard deviation is σ = $4875.
(a) What is the sample size n?
Answer: 4,225
Since

(b) What is the probability that the sample mean x̄ will be within ± $150 of the population mean µ?
Answer: 0.9545
Since

then

pnorm(2) - pnorm(-2)
## [1] 0.9544997
17. Referring to the previous exercise, demonstrate empirically that the probability that x̄ is within ±$150 of µ is 0.9545. Do not formally prove the result but rather substitute some value (any value) for µ and work out the result.
Answer:
Let µ = $100, 000, a value selected at random. Then

pnorm(100150, 100000, 75) - pnorm(99850, 100000, 75)
## [1] 0.9544997
Note: this result applies for any value of µ we might select.
18. Suppose a random sample of size n = 200 is drawn from a population with population proportion p = 0.55.
(a) What is the expected value of 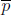 ?
?
Answer: 
(b) What is the standard error of the proportion 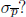 ?
?
Answer: 0.0352

19. A random sample of size n = 100 is selected from a population with p = 0.60.
(a) What is the probability that the sample proportion 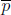 will be within ±0.02 of the population proportion? That is, what is p(0.58 ≤
will be within ±0.02 of the population proportion? That is, what is p(0.58 ≤ 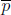 ≤ 0.62)?
≤ 0.62)?
Answer: 0.3182


#Comment. Subtract pnorm(-0.41) from pnorm(0.41).
pnorm(0.41) - pnorm(-0.41)
## [1] 0.3181941
(b) What is the probability that the sample proportion 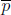 will be within ± 0.05 of the population proportion? That is, what is p(0.55 ≤
will be within ± 0.05 of the population proportion? That is, what is p(0.55 ≤ 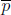 ≤ 0.65)?
≤ 0.65)?
Answer: 0.6923

#Comment. Subtract pnorm(-1.02) from pnorm(1.02).
pnorm(1.02) - pnorm(-1.02)
## [1] 0.6922715
(c) What is the probability that the sample proportion 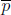 will be within ± 0.10 of the population proportion? That is, what is p(0.50 ≤
will be within ± 0.10 of the population proportion? That is, what is p(0.50 ≤ 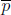 ≤ 0.70)?
≤ 0.70)?
Answer: 0.9586
p(0.50 ≤ 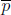 ≤ 0.70) = p(–2.04 ≤ z ≤ 2.04) = 0.9586
≤ 0.70) = p(–2.04 ≤ z ≤ 2.04) = 0.9586
#Comment. Subtract pnorm(-2.04) from pnorm(2.04).
pnorm(2.04) - pnorm(-2.04)
## [1] 0.9586497
20. A population proportion is p = 0.50. Please provide the standard error of the proportion for the following sample sizes.
(a) If n = 50, what is 
Answer: 0.0707

(b) If n = 200, what is 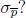
Answer: 0.0354

(c) If n = 800, what is 
Answer: 0.0177

(d) If n = 3200, what is 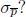 ?
?
Answer: 0.0088

21. What can we conclude about the relationship between the size of the sample n and the magnitude of the standard error of the proportion 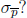 ?
?
Answer: Larger sample sizes result in smaller standard errors and greater precision. However, there are diminishing returns characterizing this relationship. In fact, for each quadrupling of the sample size, we reduce the standard error by half.
22. Assuming that the population proportion is p = 0.50, find p(0.49 ≤ 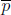 ≤ 0.51) for each of the sample sizes below.
≤ 0.51) for each of the sample sizes below.
(a) What is p(0.49 ≤ 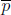 ≤ 0.51) if n = 50?
≤ 0.51) if n = 50?
Answer: 0.1124

pnorm(0.1414) - pnorm(-0.1414)
## [1] 0.112446
(b) What is p(0.49 ≤ 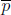 ≤ 0.51) if n = 200?
≤ 0.51) if n = 200?
Answer: 0.2227
p(0.49 ≤ 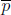 ≤ 0.51) = p(-0.2828 ≤ z ≤ +0.2828) = 0.2227
≤ 0.51) = p(-0.2828 ≤ z ≤ +0.2828) = 0.2227
pnorm(0.2828) - pnorm(-0.2828)
## [1] 0.2226698
(c) What is p(0.49 ≤ 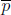 ≤ 0.51) if n = 800?
≤ 0.51) if n = 800?
Answer: 0.4284
p(0.49 ≤ 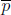 ≤ 0.51) = p(–0.5657 ≤ z ≤ +0.5657) = 0.4284
≤ 0.51) = p(–0.5657 ≤ z ≤ +0.5657) = 0.4284
pnorm(0.5657) - pnorm(-0.5657)
## [1] 0.4284023
(d) What is p(0.49 ≤ 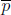 ≤ 0.51) if n = 3200?
≤ 0.51) if n = 3200?
Answer: 0.7421
p(0.49 ≤ 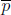 ≤ 0.51) = p(-1.1314 ≤ z ≤ +1.1314) = 0.7421
≤ 0.51) = p(-1.1314 ≤ z ≤ +1.1314) = 0.7421
pnorm(1.1314) - pnorm(-1.1314)
## [1] 0.7421132
23. The percentage of people who are lefthanded is not known with certainty but it is thought to be about 12%. Assume the population proportion of lefthanded people is p = 0.12.
(a) If a sample of n = 400 people is chosen randomly, what is the probability that the proportion of lefthanders will be within ± 0.02 of p? In other words, what is p(0.10 ≤ p ≤ 0.14)?
Answer: 0.7813
p(0.10 ≤ 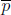 ≤ 0.14) = p(-1.23 ≤ z ≤ 1.23) = 0.7813
≤ 0.14) = p(-1.23 ≤ z ≤ 1.23) = 0.7813
pnorm(1.23)-pnorm(-1.23)
## [1] 0.7813029
(b) If a sample of n = 800 people is chosen randomly, what is the probability that the proportion of lefthanders will be within ± 0.02 of p? In other words, what is p(0.10 ≤ 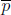 ≤ 0.14)?
≤ 0.14)?
Answer: 0.9181
p(0.10 ≤ 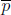 ≤ 0.14) = p(–1.74 ≤ z ≤ 1.74) = 0.9181
≤ 0.14) = p(–1.74 ≤ z ≤ 1.74) = 0.9181
pnorm(1.74)-pnorm(-1.74)
## [1] 0.918141
24. Referring to the previous exercise where we take a random sample of size n = 400, suppose we learn that the population from which we are drawing our sample consists of the entire student body of a medium-size high school in San Diego, California. The school administration is in the process of building a new auditorium, and it wants to make sure that there are a sufficient number of seats that can accommodate the lefthanded students. The entire student body is made up of 1,200 sophomores, juniors, and seniors. What is the standard error of the proportion?
Answer: 0.0133
We must use the Finite Population Correction Factor since 400/1200 = 0.3333>0.05

25. A quality control inspector is always on the lookout for substandard parts and components provided to her manufacturing company by outside suppliers. Because most shipments contain some defective items, each must be subjected to inspection. Naturally, some shipments contain more defectives than others, and it is the job of the inspector to identify the most defective-laden shipments so that they can be returned to the supplier. Suppose the inspector selects a sample of n = 100 items from a given shipment for testing. Unbeknownst to the inspector, this particular shipment includes 9% defective components. If the policy is to return any shipment with at least 5% defectives, what is the probability that this bad shipment will be accepted as good anyway?
Answer: 0.0885
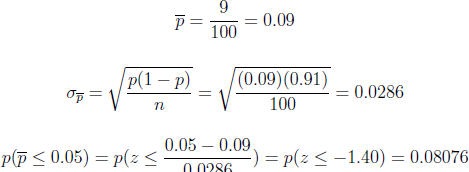
pnorm(-1.40)
## [1] 0.08075666
Thus, there is nearly a 0.081 probability that this bad shipment will sneak in as good. It should be clear that by increasing the sample size n, the inspector can reduce the probability of accepting a shipment with too many defective components. The downside to testing large samples, however, is that it is expensive and time- consuming to test large numbers of items.
![]() ≤ 0.51) for each of the sample sizes below.
≤ 0.51) for each of the sample sizes below.